AbstractThis research reports application of artificial neural network (ANN) in investigation and optimisation of boron adsorption capacity in aqueous solution using amidoxime-modified poly(acrylonitrile-co-acrylic acid) (AO-modified poly(AN-co-AA)). Both feed-forward and recurrent ANN have been utilized to predict the adsorption potential of synthesised polymer. Three operational parameters, which are adsorbent dosage, initial pH and initial boron concentration during adsorption process were designed to study their effects on the removal capacity. The ANN was trained from experimental data and serviced to optimize, develop and create various prediction models in the process of boron adsorption by AO-modified poly(AN-co-AA). Among several models, radial basis function (RBF) with orthogonal least square (OLS) algorithm displayed good prediction on boron adsorption capacity with mean square error (MSE) and coefficient of determination (R2) at 0.000209 and 0.9985, respectively. With desirable the MSE and R2 values, ANN worked as a promising prediction tool that was able to generate good estimate. The simulated maximum adsorption capacity of the synthesized polymer is 15.23 ± 1.05 mg boron/g adsorbent. Besides, from the results of ANN, the AO-modified poly(AN-co-AA) was proven to be a potential adsorbent for the removal of boron in wastewater treatment.
1. IntroductionBoron salts and boric acid have many industrial applications such as the production of porcelain and glass, manufacture of leather, carpets, cosmetic products, photographic chemical substances, fire-proofing wears as well as weatherproofing wood [1, 2]. The ion of boron sometimes present in the form of boron carbide which is usually deployed in nuclear industry as neutron radiation absorbent [3]. In addition, the isotope boron-10 is used to prevent nuclear process explosion by regulating the nuclear reaction rate [4]. This results in greater nuclear boron residue alongside development of nuclear industry. Boron impacts on human and animal reproduction system and causes irreversible damages on the nerves. Besides, overexposure of boron leads to cardiovascular and coronary systems disorders [5–7]. Therefore, the World Health Organization (WHO) recommended to industry to ensure that the concentration level of boron in the domestic water is below 0.3 mg/L [8]. In addition, the Malaysia Department of Environment (DOE) stated in local legislation that boron concentration must not exceed 1 mg/L for Effluent Discharge Standard A and 4 mg/L for Standard B [9].
In wastewater treatment, the traditional processes for boron removal those have been proposed and studied are ion exchange, solvent extraction, reverse osmosis and coagulation-precipitation, which are relatively costly in implementation and maintenance [10–11]. The utilization of AO-modified polymer through adsorption method is an attractive alternative as compared to traditional separation methods due to their high specific surface area which leads to high adsorption rate and capacity as compared to other types of materials such as foams and conventional fibers, reusability and environment-friendly attribute, etc [12–14]. The application of amidoxime-functionalized polymer in metal recovery has much been reported [15–19]. However, the possibility of incorporation of acrylic adsorbent to AO groups in adsorbing and desorbing boron ions has not been reported.
In this research, AO-modified poly(acrylonitrile-co-acrylic acid) (AO-modified poly(AN-co-AA)) was used to remove boron ions in aqueous solution through batch adsorption. AO is one of many functional groups which has high tendency to combine with wide range of heavy metal including lanthanides, actinides, poor metals as well as transition metals [20]. Nevertheless, adsorption rates of AO group are generally restricted as a result of the hydrophobic characteristic of the supporting matrix [21]. To reduce the impact of hydrophobicity, some chelating polymers have been designed by conducting the copolymerization of acrylonitrile (AN) with hydrophilic monomers. Some of the examples are acrylic acid [22, 23] and methyl acrylate [24]. In this paper, AN was polymerised with acrylic acid to minimise nitrile-nitrile interactions and hydrophobicity. Previous efforts involved the use of AO-modified adsorbent for the purpose removing selective-recovering of metals or different heavy toxic metals from numerous sources. For instance, the batch adsorption of uranium in saline water [12], cadmium and lead [14] as well as copper, nickel and manganese from aqueous solution were conducted [25].
In multivariate modelling, the artificial neural network (ANN) has proven itself to perform an helpful and competent analysis tool in latest years [26–29]. ANN is a reliable method of interpreting data through validation of manmade biological nerves and in turn computes decisions based on the existing data. ANN handles incomplete information together with more than one input-output situation. Besides, accurate prediction can be provided by ANN and does not require exact input-output data relationship. Therefore, ANN has become a preferred tool to study many non-linear or irregular models in engineering applications. It is useful particularly in the condition where the theoretical model is rather problematic to be established and the semi-empirical correlations are weakly supported [30].
There have been many studies on the modelling of heavy metal adsorption by using ANN. Among them, Turan et al. investigated Zn(II) adsorption from leachate by utilizing biosorbent. Feed forward Backpropagation (FFBPNN) neural network was applied in the study and various BP training algorithms were tried, after which their performances were compared [28]. Besides, Mitra et al. [29] applied ANN to study the equilibrium of the adsorption of Pb(II) ions by water hyacinth root. However, only a few optimization was conducted using ANN to analyse the adsorption capacity of boron. One of the research that was carried out was the boron removal using magnetic nanobeads, which applied both Response Surface Methodology (RSM) and ANN in proposing the network [31]. These are to make comparison that no research has applied ANN to analyse boron adsorption by using AO-modified poly(AN-co-AA).
The present study aimed to use MATLAB 2018a Deep Learning Toolbox to develop efficient methods based on neural networks and to apply them for estimating the boron adsorption on the AO-modified poly(AN-co-AA) under different operational parameters. Both backpropagation (Feed-forward backpropagation neural network (FFBPNN) and Cascade-forward backpropagation neural network (CFBPNN)), and layer recurrent neural network (Radial Basis Function (RBF) and nonlinear autoregressive neural network with external input (NARX)) were applied. The use of different algorithms was explored and proposed as effective network options for boron removal research. At last, the comparison was made between the predicted outputs from multiple neural network models and the experimental data. An optimisation was carried out using the best fit model and the maximum adsorption capacity of AO-modified poly(AN-co-AA) was determined.
2. Methodology2.1. Adsorbent SynthesisAcrylonitrile (AN) and acrylic acid (AA) are copolymerised into poly(acrylonitrile-co-acrylic acid) (poly(AN-co-AA)) through redox polymerisation. The reaction was performed under continuous supply of nitrogen gas inside a three-necked round-bottom flask, which was fitted with water condenser. Monomers AN (18.6 mL) and AA (1.4 mL) were added into 200 mL deionised water, followed by sodium bisulphate (SBS) (2.09 g) and potassium persulphate (KPS) (2.16 g) as initiators. The polymerisation proceeded for 2 h at constant temperature of 55°C. The chemicals were continuously stirred at 200 rpm. The polymer produced was precipitated in methanol for 1 hr, filtered and washed multiple times with deionised water and methanol successively. At last, the polymer was dried completely at 45°C in a vacuum oven until a constant weight was obtained.
In amidoxime-functionalization, 11.20 g of hydroxylamine hydrochloride (HH) was added into 320 mL of deionised water. The pH of medium was tuned to pH 7 by diluted sodium bicarbonate solution. Next, the mixture was heated at constant 70°C and stirred at 80 rpm for 1 h. Poly(AN-co-AA) (1 g) was added into the solution and was allowed to undergo amidoximation for 60 min. Finally, the modified polymer was filtered and washed repetitively, and dried in a vacuum oven constantly at 60°C for 1 d.
2.2. Experimental Adsorption StudyBoron stock solution (100 mg/L) was prepared from boric acid (H3BO3) via dissolving 5.719 g boric acid solid in 1000 mL deionised water. The impact of several physiochemical parameters which comprised of initial pH, adsorbent dosage as well as initial concentration of boron ion was studied.
In term of studying the effect of initial pH, 50 mL of 50 mg/L boric acid solution was mixed with 2 g.L−1 of adsorbent. The pH of mixture was adjusted between pH3 and pH12 by adding diluted hydrochloric acid solution (0.1 M) or sodium hydroxide solution (0.1 M). After that, the mixture was continuously shaken in digital orbital shaker Wise Shake SHO-2D (U.K.) at 150 rpm for 60 min.
In examining the effect of adsorbent dosage, 50 mg/L boron solution at default pH (pH = 7.4) was added in conical flask. Various dosage of adsorbent (0.5 g.L−1 to 4 g.L−1) was applied into the solution in each run. Meanwhile, the effect of initial concentration of boron was examined at concentration ranged between 10 mg/L to 100 mg/L. Any changes in boron concentration after the adsorption process were determined by using ICP-OES instrument.
2.3. RSMThe RSM was applied in this paper to find out the interaction effects among three factors: adsorbent dosage, pH and initial concentration of metal on boron adsorption capacity. The MATLAB version 2018a Curve Fitting Toolbox was utilized in the simulation of RSM.
2.4. Artificial Neural Network (ANN)2.4.1. Variables selectionThe adsorption process usually involves non-linear behaviour in the equilibrium mass transfer at solid-liquid interface and might involve the mass transfer limitation [11, 32]. Therefore, ANN was proposed to carry out the optimisation in boron adsorption process. In this study, initial pH value, initial concentration of boron and adsorbent dosage were set as input variables while equilibrium adsorption as output parameter. A total of 130 data points from experimental work were used as a feed to the ANN model. In the experiment, the ranges of values for pH, adsorbent dosage and initial boron concentration were 2 – 12 pH, 0.5 – 4 g/L and 10 – 100 mg/L, respectively. In the ANN simulation, the range of value for training, validation and testing sections are selected by ANN randomly within the experimental range. The range of input value was tabulated in Table 1. The neural networks were simulated in MATLAB version 2018a Deep Learning Toolbox. From the generated data fittings, the maximum adsorption capacity can be determined through optimization.
2.4.2. Model developmentThe ANN models were made up by three layers, which were respectively input layer, hidden layer at the intermediate, and the output layer (Fig. 1). The process of modelling involves multiple parameters selection, model establishment and modification, then finally results evaluation.
The model development was divided into training and testing processes. Among 130 datapoint, 70% of data point was allocated for training, 15% for testing process and the other 15% for test validation. The training process was adopted by four ANN models. Among four ANN models, two of which were back propagation: Cascade-forward back propagation neural network (CFBPNN) and Feed-forward back propagation neural network (FFBPNN). Meanwhile, another two belongs to recurrent neural network, which were nonlinear autoregressive neural network with external input (NARX) and RBF network.
In CFBPNN, FFBPNN and NARX, five different training algorithms were used in training to identify best performing ANN model on adsorption prediction. Optimization is conducted by using best algorithm after drawing benchmark comparisons.
The number of epochs was set as 100 while minimum performance was 1 × 10−3. The adsorption amount was computed by the trained model based on the data point allocated for testing process. Tangent-sigmoid (tansig) was selected as the transfer functions at the hidden layer. Linear transfer function (purelin) was practised at the output layer.
ANN training comes to a stop when one of following conditions is reached: (1) The figure of epochs (that has been set before the training) is gained; (2) The training time goes beyond the limit; (3) The gradient of performance overshoots lower limit; (4) The Marquardt parameter surpasses the constraint, or (5) Performance (Mean Square Error) (MSE)) is minimised to the target.
2.4.3. The NARX modelwhere f represents the ANN computed nonlinear function relating the adsorption, while u(t) and y(t) denote respectively the input and output data at different instant, t. Meanwhile, the network input and output order were represented by nu and ny, respectively. NARX neural network provides excellent prediction for time series data [33, 34]. NARX model has been applied in various nonlinear dynamic systems and time-series modelling [33–36]. It consists feedback networks which enclose numerous layers of the network. The ability of NARX memory to use the past predicted values allowed the network to perform well in nonlinear time series prediction [34].
Similarly, a NARX neural network is applied to speculate the boron removal capacity. Recurrent unit of 3 neurons (adsorbent dosage, pH and initial boron concentration) is within the input layer. The output layer is absorption capacity.
2.4.4. The radial basis function (RBF) modelwhere xi is the ith input; ∅︀ denotes the function; wi represents the associate weight connecting the ith node in the hidden and output layers; and || signifies the Euclidean norm.
A set of basis functions formed by weighted linear combination is called as RBF. Numerous advantages like adaptive structure, capability to generalize the ouputs to make desired predictions, fast convergence to optimum solution, independency between output values and primarily allocated weight terms, as well as good accuracy are provided by RBF [38]. The output layer performs as a linear merger in which the nonlinearity of data was displayed into another newborn linear domain [39]. The hidden layer embedded with Gaussian response functions creates a localized feedback to the feed data. Many types of RBF networks for modelling purpose has been discovered, yet the Gaussian type acquired attention from many researchers. In this form of RBF, the radial basis function can be expressed as Eq. (3) [37]:
Where r represents the length interval between data points, x and network center, c. Meanwhile, denotes parameter that control the smoothness of RBF.
2.4.5. Variation and evaluationIn most researches, two statistical errors parameters: coefficient of determination (R2) and mean square error (MSE) were involved in assessing the evaluation of the goal of the computed model. The MSE and R2 can be expressed in Eq. (4) and (5), respectively [35]:
where n is the number of sampled data, yi,pred is ith predicted value by network, yi,exp is the ith experimental value and yi,avg is the mean value of yi,exp.
3. Results and Discussions3.1. Adsorption Mechanism
Fig. 2 shows the reaction processes involve in this study which is polymerisation process, chemical modification and adsorption of heavy metal ions. In Fig. 2(a), the poly(AN-co-AA) was produced by the polymerisation process between the monomer of acrylonitrile (AN) and acrylic acid (AA). Fig. 2(b) shows the formation of AO-modified poly(AN-co-AA) after the modification process towards poly(AN-co-AA) by using hydroxylamine hydrochloride. The reactive cyano (C ≡ N) functional group was converted to amidoxime group through the nucleophilic addition reaction in order to form a high complex-forming with heavy metal ions as shown in Fig. 2(c). This proposed formation is possible due to the affinity of functional group in AO-modified poly(AN-co-AA)-modified poly(AN-co-AA) towards heavy metal ions in aqueous solution [40].
3.2. RSMIn a RSM, the three-dimensional (3-D) response surface and contour plots were simulated to study the interaction between the pH, adsorbent dosage and initial boron concentration on the adsorption capacity. The function used was polynomial with the degree of x and y both at 2. The robust mode was set to be Least Absolute Residuals (LAR).
The interactive plot of adsorbent dosage and pH was shown in Fig. 3(a). The removal of boron ions was optimum when AO-modified poly(AN-co-AA) dosage was within 4.3 – 7.4 g/L at pH ranged pH 6 – pH 9.2. The pH dependent boron uptake is mostly related to the surface functional groups of AO-modified poly (AN-co-AA). Boron can only be removed in the form of negatively charged borate ions or neutral boric acid (B(OH)3). Under the acidic condition, the surface of adsorbent became positively charged due to protonation of hydroxyl functional groups while the partial neutral adsorbent species R*OH was still present. In acidic and neutral environment, the predominant species of boron was neutral boric acid B(OH)3 [41]. Boric acid could form complex molecules with R*OH or R*OH to release H2O or H+, as represented in Fig. 2(c). On the other hand, the adsorption capacity started to reduce as the basicity was increased to more than pH 7.5. At high pH (beyond pH 7.5), boron exists mainly as borate ions (B(OH)4−) [41]; thus, electrostatic repulsion occurred between the B(OH)4− ions and the anionic adsorbents. This weakens the forces of attraction between the B(OH)4− and the negatively charged functional groups on the adsorbents, leading to a decrease in adsorption [42].
Besides, from Fig. 3(b) and (c), the adsorption capacity was higher at greater initial boron concentration but it only increases slightly after 16mg/L. It reached the peak when initial ion concentration was between 29.4 and 48.1 mg/L at pH 6 – pH 9.2. This result reveals that the active sites of adsorbents were occupied and bounded with B3+ at 40 mg/L of boron solution.
For the effect of adsorbent dosage, the removal capacity rose from 2.5 mg/g to 13.25 mg/g with an increase in the dosage from 0.5 g.L−1 to 3 g.L−1, as shown in Fig. 3(a) and 3(c). Afterwards, there was only marginally upward trend until the adsorption capacity reached its maximum between 4 g.L−1 and 7.5 g.L−1 of adsorbent dosage. At this point, the equilibrium concentration between the bounded ions to the adsorbent and unbounded ions was achieved.
3.3. Optimum Hidden NeuronThe neural network models were trained, tested and validated by experimental results under various operating conditions. The number of neurons in the hidden layer was estimated by an empirical correlation (Eq. (6)) [43]:
where Cn is the amount of neurons; Cp is the amount of input factors. Since there are 4 input variables which affect the adsorption of boron, approximately 9 neurons should be applied for the simulation. However, theoretical analysis was not enough to justify the appropriate number of neurons in the hidden layer. More accurate results were obtained by conducting trial and error from 4 to 14 neurons and comparing the performance (MSE and R2). The algorithm used at this stage was the “scaled conjugate gradient backpropagation” (SCGB) algorithm for both CFBPNN and FFBPNN while “gradient descent with momentum backpropagation” (GDMB) for NARX.
The validation analysis was performed to prevent the problem of over-fitting in the training stage. More precise training data are usually resulted from higher number of hidden neurons, but this does not work in the same way on the test data. Thus, suitable number of hidden neurons can be decided by tolerable flaw from both training and testing data. The detailed MSE (E2), and COD (R2) values for CFBPNN, FFBPNN, and NARX are listed in Table 2.
The training outcome with higher R2 and lower E2 indicates better results. Through balancing the acceptable error and complexity of the model, the optimum number of hidden neurons was 10 for FFBPNN with E2 = 0.000179 and R2 = 0.9396. Meanwhile, for CFBPNN, the optimum neuron number was 9 with E2 = 0.000231 and R2 = 0.9395. There are two optimal neuron number in NARX, which are 7 (least MSE) and 9 (highest R2). After balancing the statistical error two parameters, 9 neurons was accepted as preferable one.
3.4. Backpropagation Neural NetworkIn every model, different tested algorithms and transfer functions were tabulated in Table 3(a). The chosen performance goal was 10−5 while the total iteration was specified at 1000. In simulation using FFBPNN and CFBPNN, the scaled conjugate gradient backpropagation (SCG) algorithm provided the best fit for datapoints at R2 = 0.9396f and R2 = 0.9395 respectively, as well as lowest MSE among all algorithms. Otherwise, the Levenberg-Marquadt backpropagation (LM) and gradient descent with momentum backpropagation (GDM) also gave satisfactory results at R2 > 0.90. The results of simulation different algorithm are given in Fig. 4(a) and (b). The comparison between predicted and experimental values was displayed.
3.5. Recurrent Neural Network3.5.1. Nonlinear autoregressive model processes with exogenous input (NARX)There have been numerous modified NARX neural networks those are applied to approximate or model properties in engineering sectors [33, 35, 36]. In the current paper, a 4-9-1 NARX neural network with transfer function Tangent-sigmoid (tansig) were simulated. Responding to GDM algorithm (Gradient descent with momentum backpropagation), the bias values and weight were kept updated by this NARX training function. This network reduces the combination values of weights and squared errors, which in turn selects a suitable combination in order to yield a well generalized network.
Besides GDM algorithm, alternative training algorithms were also assessed but produced less satisfactory results. The overall training sets applied in this study was recorded in detail in Table 3(a). Fig. 5(a) displays the compatibility of experimental and predicted results as well as error histogram of the NARX model. The results unveiled the fact that the NARX neural network has the ability to forecast the adsorption of boron ions from aqueous solution by AO-modified poly(AN-co-AA) with MSE < 0.001. Therefore, the outcome is satisfactory that the presented modelling methodology can perform in future researches to solve this genre of problems.
3.5.2. RBF networkIn the RBF neural network, the widths and centers of can be generally computed by using the clustering method. The internal configuration of the neural network was adjusted dynamically by the deviation coming from the resulted clustering functions. At default, the center of the RBF neural network was chosen randomly from the arbitrary data points. The ANN rooted on RBF is trained by singular value decomposition. This method is not adequate since centers are selected non-specifically and the RBF performance relies critically on the appointed centers.
In this paper, center points were determined from orthogonal least square (OLS) algorithm. From a nominee center set, OLS algorithm chose the least-error centers at the output dataset [30]. Therefore, the problem could be solved since the selected center was satisfactory. During the RBF simulation, the coding “newrb” provided training with OLS included [44]. To reduce the error of network output, neuron of hidden layer was added by “newrb” progressively through OLS algorithm until the MSE goal was hit. Table 3(b) and Fig. 5(b) displayed the performance for RBF network. According to the standard MSE value < 0.001, the RBF network model can be applied for prediction function with realistic accuracy since the errors were normally distributed.
3.6. Comparison among Four ModelsIn analyzing the performance of all models, Fig. 3 and 4 represented the fit between the experimental data and computed data by proposed networks. The circles represent each testing datapoints that led to the network output denoted by solid straight line. In overall, the datapoints of actual vs. predicted were well distributed and were compatible with each other. Among the four network models, the RBF provided the best performance on the testing set (MSE= 0.000209 and R2 = 0.9985). This was followed by the NARX (MSE = 0.000275 and R2 = 0.9803), CFBPNN (E2 = 0.000431 and R2 = 0.9395) and lastly FFBPNN (E2 = 0.000679 and R2 = 0.9296). The RBF network with OLS function was selected after considering and weighing the acceptable errors of both training and testing data.
3.7. Determining Optimal Values by ANNAs seen in the Fig. 3 which was simulated through RSM, the relationship between the input data and the responding adsorption capacity depicted highly non-linear behavior. In this case, it was relatively difficult to estimate the optimal operating condition to reach maximum adsorption capacity. Among several solutions in optimization, ANN offers one of them. The presented network in this paper is a new attempt in developing interest in implementing ANN modelling technique into metal removal sector by using synthesized polymer.
To determine the optimum condition, variated combinations of input variables were simulated on the trained ANN [28]. The range of input was determined by the optimum range as depicted in RSM interactive plots (Fig. 3). The adsorption capacity was set as output parameters and the maximum adsorption capacity was simulated by best fit ANN. RBF neural network was selected due to the highest correlational fit and lowest error calculated in data fitting. According to the results, the ideal input values were adsorbent dosage of 4.2 g/L, initial pH of 7.8 and initial boron concentration of 41 mg/L. These input values have given removal capacity of 15.23 ± 1.050 mg boron/g adsorbent.
In optimisation, other tools such as Design of Experiment (DOE) have been widely used for statistical work. Both DOE and ANN are prevailing tools in the prediction of optimum adsorption. The DOE allows user to evaluate to influence of several parameters on the output with minimal numbers of experimental data. On the other hand, ANN possesses advantage by having a set of initial weights and adapt the weight accordingly to improve the results for data with both linearity or non-linearity [45]. ANN also does not require exact input-output relationship with strong function approximation and learning.
As compared with other adsorbent report in boron adsorption [46–52], the maximum adsorption capacity in current study at 15.23 ± 1.050 mg boron/g adsorbent has moderate performance among all. Nevertheless, this shows amidoxime-functionalized polymer as a potential alternative polymer to remove boron while the chemical structure can be further modified and improved in the future research to enhance the adsorption capacity.
4. ConclusionsThe adsorption process of boron ions by using AO-modified poly(AN-co-AA) is studied through ANN. The effects of adsorbent dosage, initial pH and initial boron concentration on the adsorption capacity were examined. The overall simulated results were matching with the experimental data with slight dissimilar. The optimal hidden neurons for FFBPNN, CFBPNN, NARX and RBF were 10, 9, 11 and 9, respectively. For the comparison among four models, the RBF model with OLS centers selection provided the most satisfactory results with MSE = 0.000209 and R2 = 0.9985. Otherwise, all other models also provide good fit with MSE < 0.001 and R2 > 0.90. The optimal operating condition for boron batch adsorption were determined as initial pH of 7.8, an adsorbent dosage of 4.2 g/L and initial concentration of 41 mg/L. The results have proven that the adsorption of boron from aqueous solution is able to be improved effectively up to 15.23 mg/g ± 1.0506. Therefore, AO-modified poly(AN-co-AA) was a considerable alternative for boron removal adsorbent. The proposed RBF model with OLS in ANN is able to describe and maximize the adsorption of boron and to support its future development.
Nomenclaturef nonlinear function y(t) input of neural network u(t) output of neural network nu network input order ny network output order xi ith input
radial basis function
wi linking weight between the ith node in the hidden and output layer c RBF network center r distance between RBF network center, c and data points, x σ parameter that control the smoothness of RBF n number of sampled data yi,pred ith predicted value by network yi,exp ith experimental value yi,avg mean value of yi,exp
AcknowledgmentThe authors would like to express gratitude to the Ministry of Higher Education Malaysia for the financial support provided under the Fundamental Research Grant Scheme (FRGS) project code FRGS/1/2013/SG01/UPM/02/3 (02-01-13-1215FR) Vote 5524296. Thanks are due to the Chemistry Department, Faculty of Science, Universiti Putra Malaysia and Department of Chemical and Environmental Engineering, Faculty of Engineering, Universiti Putra Malaysia, for providing research facilities.
NotesAuthor Contributions L.K.L (Master student) performed all the experimental and involved in data analysis. S.N.A.M.J. (Associate Professor), L.C.A. (Professor), N.N.L.N.I. (Senior Lecturer), M.N. (Senior Lecturer) and A.A.A. (Ph.D) involved in data analysis. S.N.A.M.J. (Ph.D), L.C.A. (Ph.D) and M.N. (Ph.D) contributed reagents, materials and analysis tools. All authors have read and agreed to the published version of the manuscript. References1. Nasef MM, Nallappan M, Ujang Z. Polymer-based chelating adsorbents for the selective removal of boron from water and wastewater: A review. React Funct Polym. 2014;85:54–68.
2. Köse TE, Demiral H, Öztürk N. Adsorption of boron from aqueous solutions using activated carbon prepared from olive bagasse. Desalin Water Treat. 2011;29:1–3.
3. Domnich V, Reynaud S, Haber RA, Chhowalla M. Boron carbide: Structure, properties, and stability under stress. J Am Ceram Soc. 2011;94:3605–3628.
4. Wang B, Guo X, Bai P. Removal technology of boron dissolved in aqueous solutions - A review. Colloids and Surfaces A: Physicochem Eng Asp. 2014;444:338–344.
5. Cengeloglu Y, Arslan G, Tor A, Kocak I, Dursun N. Removal of boron from water by using reverse osmosis. Sep Purif Technol. 2008;64:141–146.
6. Guan Z, Lv J, Bai P, Guo X. Boron removal from aqueous solutions by adsorption - A review. Desalination. 2016;383:29–37.
7. Wolska J, Bryjak M. Methods for boron removal from aqueous solutions - A review. Desalination. 2013;310:18–24.
8. WHO. Boron in drinking-water background document for development of WHO guidelines for drinking-water quality [Internet]. Iris: WHO; c1998. [cited 2 Februrary 1998]. Available from: https://apps.who.int/iris/handle/10665/70170
9. Department of Environment, Environmental Requirements : A Guide for Investors. Minist Nat Resour Environ. 2010;1–14.
10. Hilal N, Kim GJ, Somerfield C. Boron removal from saline water: A comprehensive review. Desalination. 2011;273:23–35.
11. Vasudevan M, Ajithkumar PS, Singh RP, Natarajan N. Mass transfer kinetics using two-site interface model for removal of Cr ( VI ) from aqueous solution with cassava peel and rubber tree bark as adsorbents. Environ Eng Res. 2016;21:152–163.
12. Gunathilake C, Gorka J, Dai S, Jaroniec M. Amidoxime-modified mesoporous silica for uranium adsorption under seawater conditions. J Mater Chem A. 2015;3:11650–11659.
13. Saeed K, Haider S, Oh TJ, Park SY. Preparation of amidoxime-modified polyacrylonitrile (PAN-oxime) nanofibers and their applications to metal ions adsorption. J Memb Sci. 2008;322:400–405.
14. Zahri NAM, Siti NA, Abdullah LC, Thomas SYC. Improved method for preparation of amidoxime modified poly(acrylonitrile-co-acrylic acid): Characterizations and adsorption case study. Polymers (Basel). 2015;7:1205–1220.
15. Satilmis B, Isık T, Demir M, Uyar T. Amidoxime functionalized Polymers of Intrinsic Microporosity (PIM-1) electrospun ultrafine fibers for rapid removal of uranyl ions from water. Appl Surf Sci. 2019;467–468:628–657.
16. Zhibin Z, Dong Zhimin, Wang Xuangxue, et al. Ordered mesoporous polymer–carbon composites containing amidoxime groups for uranium removal from aqueous solutions. Chem Eng J. 2018;341:208–217.
17. Puspitasari T, Kadja GTM, Radiman CL, Darwis D, Mukti RR. Two-step preparation of amidoxime-functionalized natural zeolites hybrids for the removal of Pb2+ ions in aqueous environment. Mater Chem Phys. 2018;216:197–205.
18. Siming L, Lifeng C, Hamza MF, et al. Amidoxime functionalization of a poly(acrylonitrile)/silica composite for the sorption of Ga(III) – Application to the treatment of Bayer liquor. Chem Eng J. 2019;368:459–473.
19. Adio SO, Asif M, Mohammed ARI, Baig N, Al-Arfaj AA, Saleh TA. Poly (amidoxime) modified magnetic activated carbon for chromium and thallium adsorption: Statistical analysis and regeneration. Process Saf Environ Prot. 2019;121:254–262.
20. Alakhras FA, Dari KA, Mubarak MS. Synthesis and chelating properties of some poly(amidoxime-hydroxamic acid) resins toward some trivalent lanthanide metal ions. J Appl Polym Sci. 2005;97:691–696.
21. Ji C, Qu R, Chen H, Liu X, Sun C, Ma C. Hg(II) adsorption using amidoximated porous acrylonitrile/itaconic copolymers prepared by suspended emulsion polymerization. Water Sci Technol. 2016;73:1709–1718.
22. Oyola Y, Dai S. High surface-area amidoxime-based polymer fibers co-grafted with various acid monomers yielding increased adsorption capacity for the extraction of uranium from seawater. Dalt Trans. 2016;45:8824–8834.
23. Xing Z, Jiangtao H, MouHua W, et al. Properties and evaluation of amidoxime-based UHMWPE fibrous adsorbent for extraction of uranium from seawater. Sci China Chem. 2013;56:1505–1509.
24. Liu X, Chen H, Wang C, Ji C, Sun C, Zhang Y. Synthesis of porous acrylonitrile/methyl acrylate copolymer beads by suspended emulsion polymerization and their adsorption properties after amidoximation. J Hazard Mater. 2010;175:1014–1021.
25. El-Bahy SM, El-Bahy ZM. Synthesis and characterization of polyamidoxime chelating resin for adsorption of Cu(II), Mn(II) and Ni(II) by batch and column study. J Environ Chem Eng. 2016;4:276–286.
26. Bingöl D, Hercan M, Elevli S, Kiliç E. Comparison of the results of response surface methodology and artificial neural network for the biosorption of lead using black cumin. Bioresour Technol. 2012;112:111–115.
27. Zafar M, Vinh NV, Behera SK, Park HS. Ethanol mediated As(III) adsorption onto Zn-loaded pinecone biochar: Experimental investigation, modeling, and optimization using hybrid artificial neural network-genetic algorithm approach. J Environ Sci China. 2017;54:114–125.
28. Turan NG, Mesci B, Ozgonenel O. Artificial neural network (ANN) approach for modeling Zn(II) adsorption from leachate using a new biosorbent. Chem Eng J. 2011;173:98–105.
29. Mitra T, Singha B, Bar N, Das SK. Removal of Pb(II) ions from aqueous solution using water hyacinth root by fixed-bed column and ANN modeling. J Hazard Mater. 2014;273:94–103.
30. Turan NG, Mesci B, Ozgonenel O. The use of artificial neural networks (ANN) for modeling of adsorption of Cu(II) from industrial leachate by pumice. Chem Eng J. 2011;171(3)1091–1097.
31. Oladipo AA, Gazi M. Targeted boron removal from highly-saline and boron-spiked seawater using magnetic nanobeads: Chemometric optimisation and modelling studies. Chem Eng Res Des. 2017;121:329–338.
32. Vasudevan M, Kumar GS, Nambi IM. Numerical studies on kinetics of sorption and dissolution and their interactions for estimating mass removal of toluene from entrapped soil pores. Arab J Geosci. 2015;8:6895–6910.
33. Çoruh S, Geyikçi F, Kiliç E, Çoruh U. The use of NARX neural network for modeling of adsorption of zinc ions using activated almond shell as a potential biosorbent. Bioresour Technol. 2014;151:406–410.
34. Boussaada Z, Curea O, Remaci A, Camblong H, Bellaaj NM. Prediction of the daily direct solar radiation using nonlinear autoregressive exogenous (narx) network model. Energies. 2018;11:620.
35. Ghaedi AM, Vafaei A. Applications of artificial neural networks for adsorption removal of dyes from aqueous solution: A review. Adv Colloid Interface Sci. 2017;245:20–39.
36. Abdalkader SA, Omaima NAA. Nonlinear autoregressive neural network for estimation soil temperature : A comparison of different optimization neural network. In : ICIT 2011 Conference; October 2011; Jordan. p. 43–51.
37. Mohebbi A, Ahmadi-Pour M, Mohebbi M. Accurate prediction of liquid phase equilibrium adsorption of sulfur compound. Chem Eng Res Des. 2017;126:199–208.
38. Xia C, Wang J, McMenemy K. Short, medium and long term load forecasting model and virtual load forecaster based on radial basis function neural networks. Int J Electr Power Energ Syst. 2010;32:743–750.
39. Tatar A, Shokrollahi A, Mesbah M, Rashid S, Arabloo M, Bahadori A. Implementing Radial Basis Function Networks for modeling CO2-reservoir oil minimum miscibility pressure. J Nat Gas Sci Eng. 2013;15:82–92.
40. Shaaban AF, Fadel DA, Mahmoud AA, Elkomy MA, Elbahy SM. Synthesis of a new chelating resin bearing amidoxime group for adsorption of Cu(II), Ni(II) and Pb(II) by batch and fixed-bed column methods. J Environ Chem Eng. 2014;2:632–641.
41. Wei Y, Zheng Y, Chen JP. Design and fabrication of an innovative and environmental friendly adsorbent for boron removal. Water Res. 2011;45:2297–2305.
42. Kiani GR, Sheikhloie H, Arsalani N. Heavy metal ion removal from aqueous solutions by functionalized polyacrylonitrile. Desalination. 2011;269:266–270.
43. Li W, Wei S, Jiao W, Qi G, Liu Y. Modelling of adsorption in rotating packed bed using artificial neural networks (ANN). Chem Eng Res Des. 2016;114:89–95.
44. Luo H, Zhou T, Gong J. Radial Basis Function Neural Network for Soil Classification in Hilly [dissertation]. China: MIPPR 2005 SAR and Multispectral Image Processing; 2005.
45. Kukreja H, Bharath N, Siddesh CS, Kuldeep S. An introduction to artificial neural network. Inter J Adv Res Innov Ideas Edu. 2016;1:27–30.
46. Harada A, Takagi T, Kataoka S, Yamamoto T, Endo A. Boron adsorption mechanism on polyvinyl alcohol. Adsorption. 2011;17:171–178.
47. Harada A, Takagi T, Kawai A, Endo A. Effect of synthesis conditions of polyallylamine-beads-glucose (PAA-Glu) on boron adsorption. Adsorption. 2013;19:1–9.
48. Li X, Liu R, Wu S, Liu J, Cai S, Chen D. Efficient removal of boron acid by N-methyl-D-glucamine functionalized silica-polyallylamine composites and its adsorption mechanism. J Colloid Interface Sci. 2011;361:232–237.
49. Ting TM, Hoshina H, Seko N, Tamada M. Removal of boron by boron-selective adsorbent prepared using radiation induced grafting technique. Desalin Water Treat. 2013;51:2602–2608.
50. Sanfeliu C, Martinez-Manez R, Sancenon F, et al. 11B-MAS NMR approach to the boron adsorption mechanism on a glucose-functionalised mesoporous silica matrix. Microporous Mesoporous Mater. 2018;266:232–241.
Fig. 2(a) Polymerisation of poly(AN-co-AA) (b) Formation of amidoxime (AO)-modified poly(AN-co-AA) (c) Complex formation of boron ion with AO modified poly(AN-co-AA) 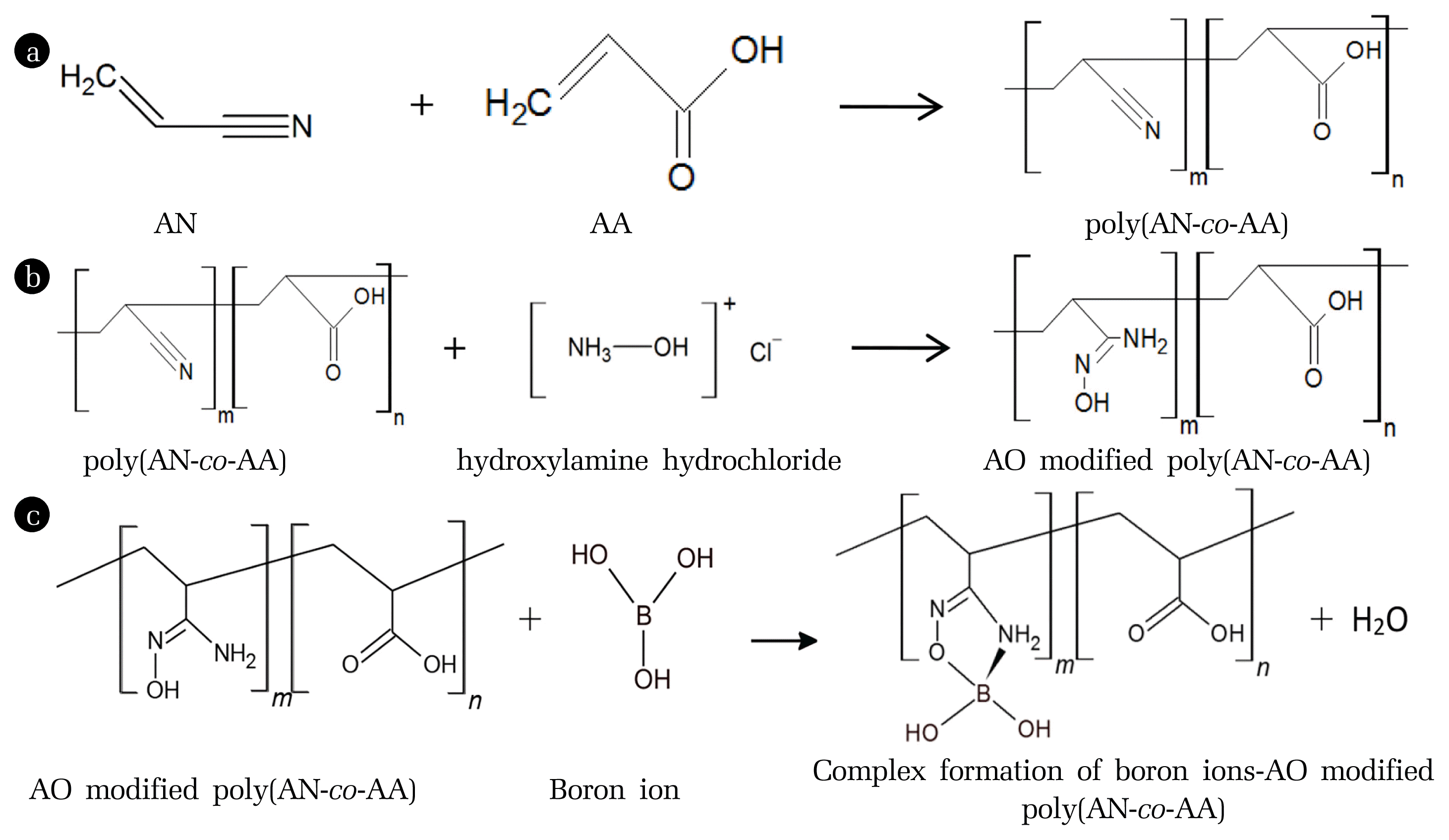
Fig. 4Comparison between experimental and predicted results using (a) FFBPNN with SCG algorithm and (b) CFBPNN with SCG algorithm 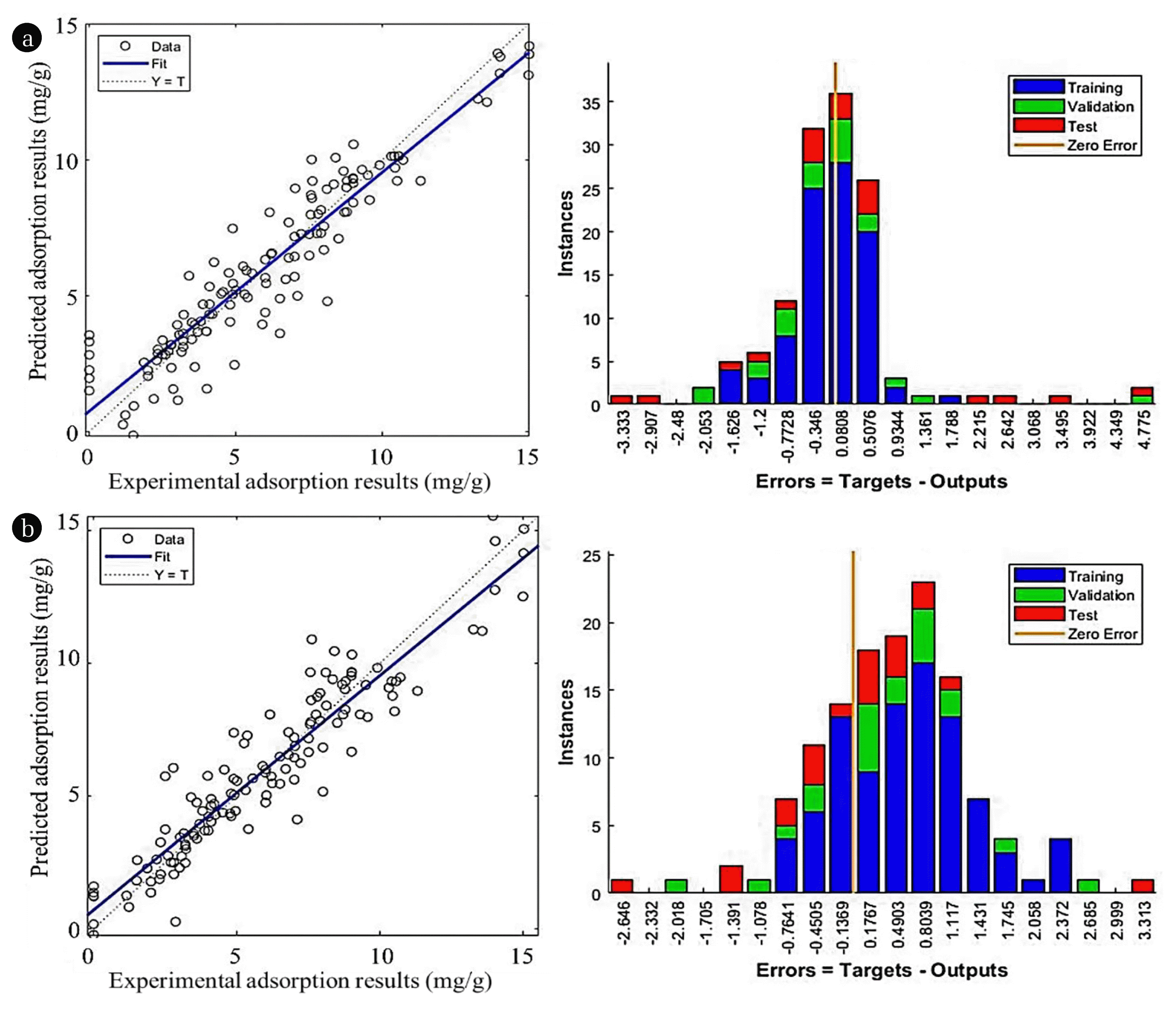
Fig. 5Comparison between experimental and predicted results using (a) NARX with GDM algorithm (b) RBF with OLS parameters selection 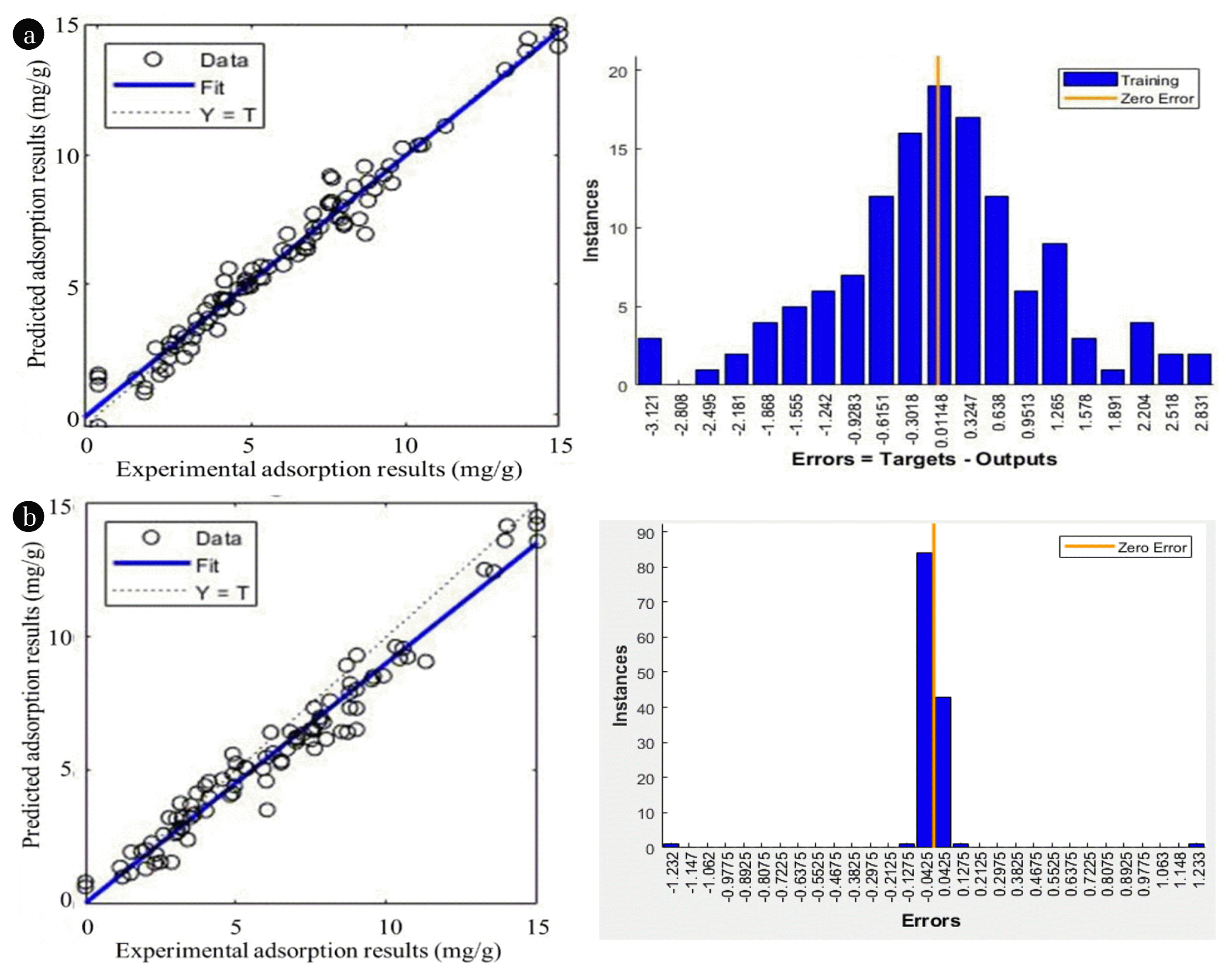
Table 1The Scope of Feed Data in ANN Table 2Performance of Each Model at Different Number of Neurons Table 3(a) Performance of NARX Neural Network When Used with Different Training Algorithms
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||