1. Introduction
Recently, there have been frequent occurrences of algal blooms owing to climate change and rising water temperatures (WTs), leading to a rising interest in water quality management of rivers and reservoirs owing to physical environmental changes. Such algal blooms not only threaten the aquatic ecosystem but also have direct and indirect influences on human life; therefore, solving this problem is extremely important [1–2]. Algal blooms are influenced by a variety of factors including those influencing water quality, such as increasing nutrients and changing WT, as well as climate factors such as air temperature, solar radiation (SR), and precipitation [3–4]; there are ongoing studies to discover the factors influencing algal blooms. However, there are limitations to presenting clear causal relationships between influential factors pertaining to algal blooms, given a complex web of influence from environmental factors as well as the differences in their characteristics by region and period.
One of algal bloom management methods is to predict through numerical modeling considering various influential factors such as WT and nutrients. However, there are some difficulties associated with numerical modeling such as the requirement of large amounts of data, time to construct the inputs required for modeling, as well as large uncertainties associated with model parameters [5–6]. To resolve these issues, there are ongoing studies on algal bloom prediction using machine learning methods, such as the data-based artificial neural network (ANN) and model trees (MTs). Park et al. [7] used an ANN and a support vector machine (SVM) to predict chlorophyll-a concentration for providing early warning in the Juam reservoir and Yeongsan reservoir, which are located in an upstream region (freshwater reservoir) and a downstream region (estuarine reservoir), respectively. Jung et al. [8] tested and proposed M5 MTs using partial least-squares regression (PLSR) on a particular dataset and then compared the results to those obtained using M5 MTs, MLF- and RBF-ANN, and k nearest neighbors (kNN). Ye et al. [9] presented an integrated system for real-time observation, early warning, and forecasting of phytoplankton blooms by integrating automated online sondes and an ecological model. Lee et al. [10] suggested that an ANN model with a small number of input variables can capture the trends of algal dynamics, but data with a minimum sampling interval of one week are necessary. Kim et al. [11] proposed an effective method for establishing algal bloom forecasting models using ANNs. Recently, among the various machine learning methods, the extreme learning machine (ELM) method has been proven to have quick learning speeds and high performance; it is being used for predictive modeling in various areas such as predicting power supply stability, river flooding, and algal blooms. Xu et al. [12] developed an ELM-based predictor for real-time frequency stability assessment to enhance the dynamic security of power systems. Yadav et al. [13] studied a new technique, online sequential extreme learning machine (OS-ELM) that is capable of updating the model equation based on new data entry without much increase in computational cost for flood forecasting; the performance of the OS-ELM was comparable to those of other widely used artificial intelligence (AI) techniques like SVMs, ANNs and genetic programming (GP). Lou et al. [14] attempted to develop an ELM-based predictive model to simulate the dynamic change in phytoplankton abundance in Macau reservoir, given a variety of water variables. Boyer et al. [15] assessed the chlorophyll-a indicator as being relevant and reflecting the state of the Florida Bay ecosystem; this indicator is sensitive to ecosystem drivers (stressors, especially nutrient loading), feasible to monitor, and scientifically defensible.
Algal blooms tend to change over short terms given climatic conditions, polluting matter, and hydraulic characteristics; as such, these characteristics have led to various policies or studies that observe algal blooms through real-time monitoring. The real-time monitoring of chlorophyll-a concentration, an indicator of algal blooms, was presented as an effective method to predict algal blooms [15]; the monitoring data were applied in machine learning to develop short-term algal bloom prediction models.
In this study, we developed two short-term algal bloom prediction models for the Juksan weir, located downstream from the Yongsan River. Real-time water quality measurement data were applied in M5P and ELM for developing algal bloom prediction models. Furthermore the optimal data structure for input-output was determined. We compared the performance of M5P and ELM for developing short-term chlorophyll-a concentration prediction models (1–7 d). It is expected that the data-based chlorophyll-a concentration prediction model developed in this study would be useful in predicting the influential factors and size of algal blooms.
2. Materials and Methods
2.1. Study Area
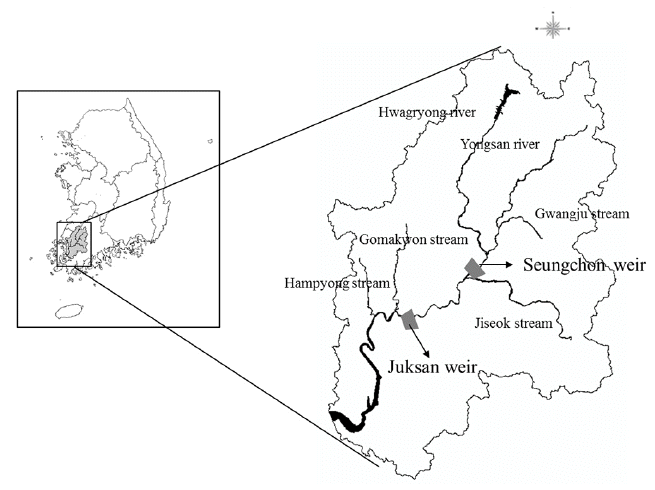
The Juksan weir in the Youngsan River, situated in South Korea, was selected as the study area with length and watershed area being 129.5 km and 3,455 km2, respectively. The representative tributaries in the watershed include the Hwangryong River with a basin area of 564.3 km2 and the Jiseok stream with a basin area of 657.2 km2. Fig. 1 shows the Juksan weir locations of the Youngsan River in South Korea and the watershed area. The Youngsan River has two weirs (Seungchon weir and Juksan weir), which were built in sequence from 2012. Particularly, the Juksan weir of the lower Youngsan River has harmful algal bloom every summer. These algal blooms can cause water treatment problems for agricultural water supply, residential drinking water, and industrial water supply. Furthermore, the chlorophyll-a concentration in winter is higher than other rivers in Korea. Harmful algal bloom means toxic, hypoxia-generating cyanobacterial bloom genera, and it is controlled by the synergistic effects of nutrient (nitrogen and phosphorus) supplies, light, temperature, water residence, and biotic interactions [4].
Water quality data in this study were obtained from a real-time water quality monitoring station called Naju. This station, operated by Korean Ministry of Environment, was monitored on a daily basis from January 2013 to December 2016, and the database is managed by Real-Time Water Quality Information System. The chlorophyll-a concentration at the Naju real-time water quality station, which is located upstream 1 km from the Juksan weir was averaged 39.8 μg/L from 2013 to 2016, and the maximum concentration was 206.2 μg/L in August 2016. Table 1 shows the statistical values of water qualities such as chlorophyll-a concentration, WT, total nitrogen (T-N), and total phosphorus (T-P). Ecosystems can be classified into trophic categories using nutrients and algal biomass through various methods. The boundaries placed between these categories by aquatic scientists are similar but not universal. The US EPA suggested a eutrophic state based on values of annual average chlorophyll-a concentration exceeding 35 μg/L [16]. Accordingly, the Juksan weir can be considered as the eutrophic state, where the yearly average chlorophyll-a concentrations were 40.7, 36.0, 38.4, 44.1 μg/L in 2013, 2014, 2015, and 2016, respectively.
The T-P concentration averaged 0.101 mg/L, which exceeded the OECD eutrophication standards of T-P concentration of 0.035 mg/L [17]. This study collected climate data separately from the water quality data to analyze their correlation with chlorophyll-a concentration, an indicator of algal blooms; the correlation between each item and chlorophyll-a was found to be low. The T-N and N/P ratios had positive correlations, whereas T-P, WT, rainfall (RF), and SR had negative correlations with low degrees of correlations.
2.2. Algorithms
2.2.1. M5P model tree
MTs, although simple, are efficient and accurate tools for modeling the patterns and relationships for large datasets [18]. Quinlan et al. [19] developed a new type of tree called the M5 tree to predict continuous variables. An over-fitting problem can occur during MT construction based on training data. Predictably, the accuracy of the tree for training examples increases monotonically as the tree grows. However, this increases over-fitting; thus, the accuracy measured over the independent test examples first increases, then decreases. A method for reducing this problem is called “pruning.” The final stage is to use a smoothing process to compensate for sharp discontinuities that inevitably occur between adjacent linear models at the leaves of the pruned tree, particularly for some models constructed from a small number of training instances. The smoothing procedure described by Quinlan et al. [19] uses the leaf model to compute the predicted value. The value is then filtered along the path back to the root, smoothing it at each node by combining it with the value predicted by the linear model for that node. In summary, the three major steps for M5 tree development are (1) tree construction; (2) tree pruning; and (3) tree smoothing. The M5 tree construction process attempts to maximize a measure called the standard deviation reduction (SDR). SDR is defined as
where T is the set of cases, Ti is the ith subset of cases that result from the tree splitting based on a set of variables (attributes), sd(T) is the standard deviation of T, and sd(Ti) is the standard deviation of Ti as a measure of error [20].
Wang et al. [21] modified the original M5 tree algorithm to handle enumerated attributes and attribute missing values; they called the new tree algorithm “the M5P algorithm”. In the M5P tree algorithm, all enumerated attributes are transformed into binary variables before tree construction. This algorithm can effectively deal with missing values and enumerated attributes. The M5P tree algorithm has three main steps, namely building the tree, pruning the tree, and smoothing. The basic tree is formed using the splitting criterion, which treats the standard deviation of the class values that reach a node as a measure of the error at that node, and calculates the expected reduction in error as a result of testing each attribute at that node. The attribute that maximizes the expected error reduction is then selected. The M5P MT has only recently been introduced in the water sector and has not yet been widely applied [8, 22].
2.2.2. Extreme learning machine
ELM is a new type of single-hidden-layer feed-forward network (SLFN) [23–25]. The Moore-Penrose generalized inverse and the minimum norm least-squares solution of a general linear system play important roles in the ELM learning algorithm. A general linear system Ax = y in Euclidean space, where A ∈ Rm×n and y ∈ Rm. Given a set of N samples (xi, ti), i = 1, 2, . . . , N, where xi = [xi1, xi2, . . . , xin]T ∈ Rn and ti = [ti1, ti2, . . ., tim]T ∈ Rm, standard SLFNs with Ñ hidden neurons and activation function g(x) are mathematically modeled as
where wi = [wi1, wi2, · · ·, wim]T is the weight vector connecting the ith hidden neuron and the input neurons, βi = [βi1, βi2, · · ·, βim]T is the weight vector connecting the ith hidden neuron and the output neurons, and bi is the threshold of the ith hidden neuron. wi·xj denotes the inner product of wi and wj.
The standard SLFNs with hidden neurons with activation function g(x) can approximate these N samples with zero error, i.e., there exist βi, wi, and bi such that
The above N equations can be written compactly as
where
2.3. Model Development
Chlorophyll-a was used as the primary indicator for algal blooms. Other water qualities monitored were WT, pH, dissolved oxygen, electrical conductivity, turbidity, T-N, T-P, and total organic carbon. Weather data in this study were obtained from the Gwangju station monitored by the Korea Meteorological Administration. Table 2 shows the input variations, periods, and sources.
To analyze the inter-period correlation within the time-series data with chlorophyll-a, a serial correlation analysis (SCA) was conducted [11]. The analysis results indicated that the chlorophyll-a concentration of the target day had a correlation coefficient of 0.90 with 1-day-ahead chlorophyll-a concentration (CHL1), 0.70 with 3-days-ahead chlorophyll-a concentration (CHL3), 0.61 with 5-days-ahead chlorophyll-a concentration (CHL5) and 0.52 with 7-days-ahead chlorophyll-a concentration (CHL7). It was expected that the previous chlorophyll-a observation data would be variable in order to raise the predictability of the model, and using chlorophyll-a concentration 1–7 d before the model was utilized was expected to help construct the short-term algal bloom predictive model (Table S1).
In order to develop the algal bloom prediction model, independent parameters in the dataset include WT, RF, SR, T-N, T-P, N/P ratio, and chlorophyll-a as M5P MT and ELM model input. The nutrients N and P are the most important limiting factors influencing productivity. Moreover, the chlorophyll-a concentration increased with high P or N and low N/P ratio that supports some previous studies in a lotic environment [28–29]. Daily chlorophyll-a concentration was used as the model output that was the primary indicator of algal blooms. Parameters were selected considering input minimization and optimization [5–6, 30]. Both M5P MT and ELM were designed to predict the chlorophyll-a concentration after 1, 3, 5, and 7 d in terms of short-term algal bloom prediction. Table S2 shows the model input variables for short-term algal bloom prediction.
A total of 50% of the dataset were applied for model training and the remaining 50% were applied for model testing to develop algal bloom prediction model by each weir. The performance of the models for the Juksan weir was evaluated using the following indicators: square of correlation coefficient (R2) that provides the variability measure for the data reproduced in the model; root-mean-square error (RMSE) that measures residual errors, providing a global idea of the difference between observation and modeling. The indicators were defined as shown below through Eq. (7) and (8).
A total of 50% of the dataset were applied for model training and the remaining 50% were applied for model testing to develop algal bloom prediction model by each weir. In two equations, n is the number of data; Yi are Ȳi are observation data and the mean of observation data, respectively; and Y̑ denotes the model ling results.
3. Results
3.1. M5P Model Results
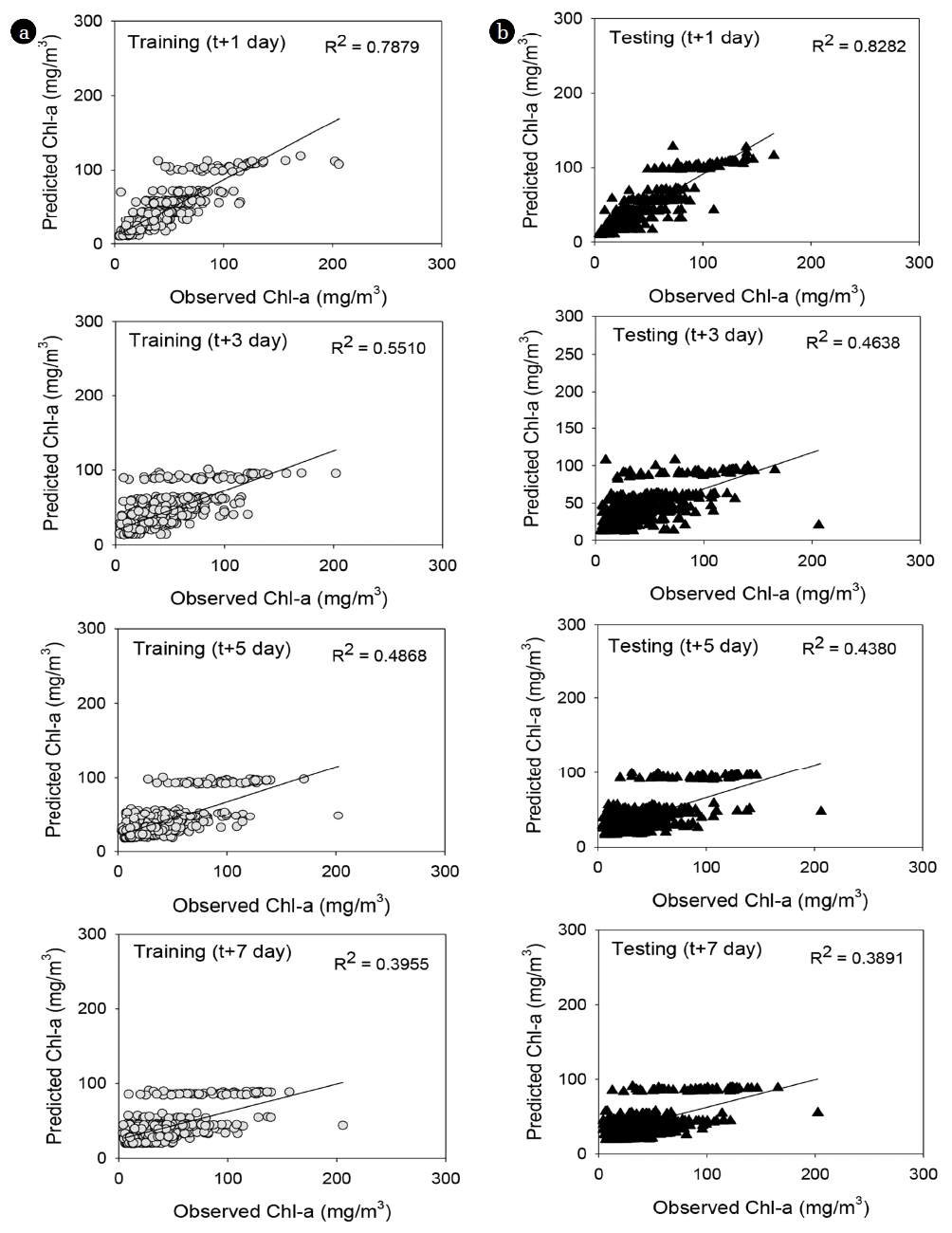
The algal bloom prediction model using the M5P MT was constructed based on the daily real-time water quality and weather data collected from 2013 to 2016. Of the collected data set orders, odd-numbered orders were utilized for training, and even-numbered orders were used for testing. The M5P MT was applied to develop the algal bloom prediction model to predict chlorophyll-a concentration after 1, 3, 5, and 7 d. In the present paper, the M5P algorithm implemented in Weka software (version 3.9.1 1999–2016) was used. This algorithm results were then evaluated using R2 and RMSE. The performance of the M5P models is shown in Fig. 2. The performance of the model to predict chlorophyll-a concentration after 1 d has R2 values of 0.79 for training and 0.83 for testing data sets and RMSE values of 14.0 μg/L for training and 12.2 μg/L for testing data sets. The performance of the model to predict chlorophyll-a concentration after 3 d has R2 values of 0.55 for training and 0.46 for testing data sets and RMSE values of 20.0 μg/L for training and 22.1 μg/L for testing data sets, indicating a lower predictive power compared with that of the prediction model after 1 d. The performance of the model to predict chlorophyll-a concentration after 5 d has R2 values of 0.49 for training and 0.44 for testing data sets, and RMSE values of 21.3 μg/L for training and 22.6 μg/L for testing data sets. The performance of the model to predict chlorophyll-a concentration after 7 d has R2 values of 0.40 for training and 0.39 for testing data sets and RMSE values of 23.5 μg/L for training and 23.5 μg/L for testing data sets.
We compared the equation’s independent variables developed by M5P for each model to predict chlorophyll-a after 1, 3, 5, 7 d. For the prediction model after 1 d, only chlorophyll-a was selected as the independent variable. Furthermore, the WT, SR, RF, and chlorophyll-a were selected as independent variables to predict chlorophyll-a after 3 d. The WT, SR, chlorophyll-a were selected as independent variables to predict chlorophyll-a after 5 d. Furthermore, the WT, SR, T-N, N/P ratio, and chlorophyll-a were selected as independent variables to predict chlorophyll-a after 7 d. The short-term algal bloom prediction model using M5P indicated that the performance of the 1 d prediction model was the highest. As the predictive periods increased to 3, 5 and 7 d, the number of independent variables included in the predictive equation increased. Moreover, prediction of 3 and 5 d periods included weather data, and the 7 d period included nutrient data (Table S3). The M5P method is based on classification and regression analysis. Comparing the measured and predicted values of the concentration of chlorophyll-a, the independent variables can help in calculating the concentration of chlorophyll-a within a certain range.
3.2. ELM Model Results
In this study, we also developed a short-term algal bloom prediction model for Juksan weir using ELM with the same water quality and weather data from 2013 to 2016 used in M5P. In the present study, the ELM algorithm was implemented in MATLAB software. Similar to M5P, among the collected data set orders, the odd number orders were utilized for training, while the even numbers were used for testing and constructing the models to predict chlorophyll-a concentration after 1, 3, 5, 7 d. ELM models were constructed in order to determine the optimum number of nodes in the hidden layer. The number of hidden nodes is determined when the performance of the test set for model validation reaches a minimum while the number of hidden node increases from 2 to 20. The training and testing performance of the ELM are shown in Fig. S1.
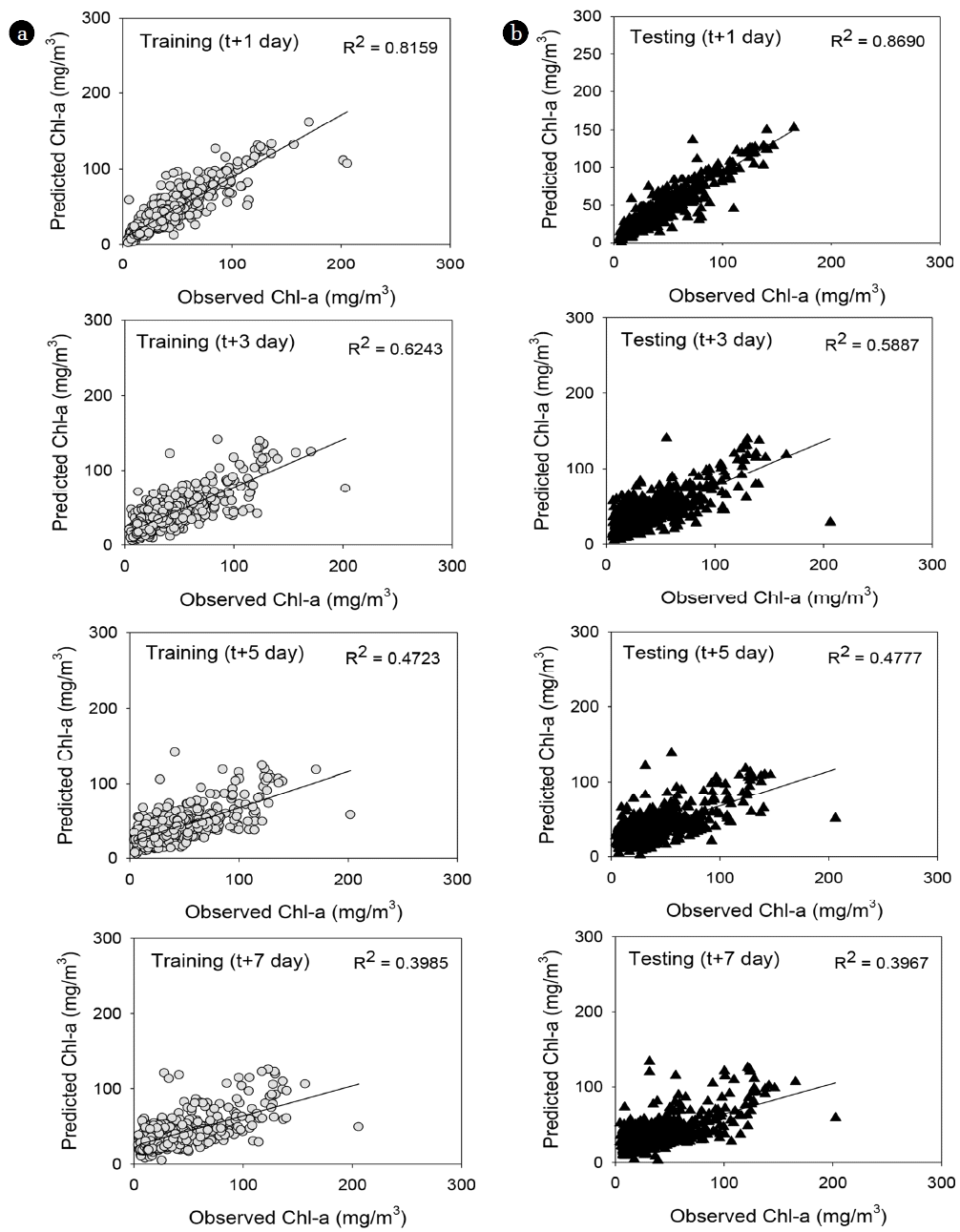
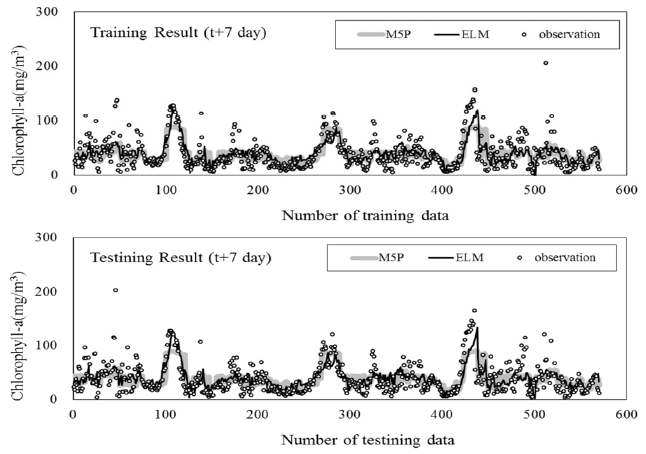
The performance power of the model to predict chlorophyll-a after 1 d has R2 of 0.82 for training and 0.87 for testing data sets, RMSE of 13.0 μg/L for training and 10.7 μg/L for testing data sets. The performance power of the model to predict chlorophyll-a after 3 d has R2 of 0.62 for training and 0.59 for testing data sets, RMSE of 18.3 μg/L for training and 19.4 μg/L for testing data sets, indicating lower performance power compared to model to predict chlorophyll-a after 1 d. The performance power of the model to predict chlorophyll-a after 5 d has R2 of 0.47 for training and 0.48 for testing data sets, RMSE of 21.6 μg/L for training and 21.8 μg/L for testing data sets. And performance power of the model to predict chlorophyll-a after 7 d has R2 of 0.40 for training and 0.40 for testing data sets, RMSE of 23.4 μg/L for training and 23.3 μg/L for testing data sets. The performance of the ELM model is shown in Table 3 and Fig. 3.
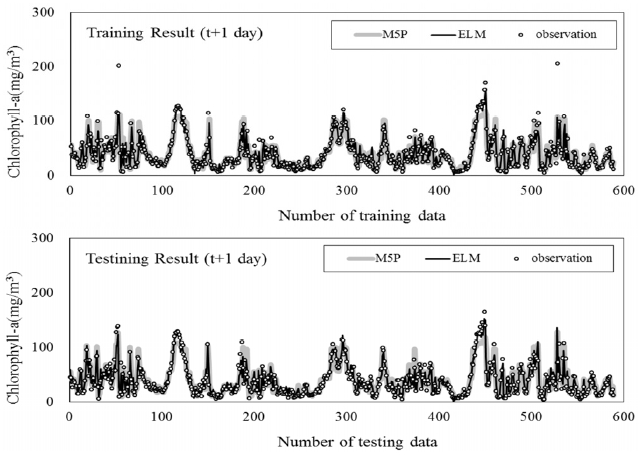
The performance power of the ELM model was higher than that of M5P model. In addition, during the period when the chlorophyll-a concentration increased rapidly, the ELM model had higher accuracy than did the M5P model; this difference was more pronounced for longer prediction periods (Figs. 4, S2. S3, 5). As the M5P model presents independent variable that influence variations in chlorophyll-a, it is useful for determining influencing factors for algal blooms. However, the accuracy of this model decreases with an increase in the prediction periods for algal bloom prediction models. As such, the ELM model appears to be more appropriate for predicting the chlorophyll-a concentration within 7 d.
4. Conclusions
We applied the M5P MT and ELM to develop a data-based model for short-term algal bloom prediction at Juksan weir, and developed 1, 3, 5, 7 d short-term prediction models. Chlorophyll-a concentration, which was the primary indicator of the algal bloom prediction model, was used to develop and compare the algal bloom models. The input variables included T-N, T-P, N/P ratio, WT, chlorophyll-a, RF, and SR. The results of the autocorrelation analysis for chlorophyll-a indicated that previous measurements of chlorophyll-a would serve as a good variable to increase the performance power of the prediction model. 50% of the dataset was applied for model training, while the remaining 50% was applied for model testing to develop the algal bloom prediction model. M5P model showed that the prediction model after 1 d had the highest performance power and dropped off rapidly starting with prediction after 3 d. Comparing the variables used in M5P model equations depending, for the prediction after 1 d chlorophyll-a concentration, value yielded was the chlorophyll-a concentration as measured 1 d ago; for the prediction model after 3 and 5 d, they included weather data, and the prediction model after 7 d also added nutrients. The present study has analyzed the performance power of ELM model; the prediction model after 1 d had the highest performance power. Comparing the performance power of the ELM model with the M5P model, it was found that the predictive power of the 1–7 d chlorophyll-a concentration prediction model was higher. Moreover, in a period of rapid algal blooms increases, the ELM model had higher accuracy than MT; this difference was more pronounced with longer prediction periods. As the M5P model presents the independent variable that influences changes in the chlorophyll-a concentration, it is useful for determining affecting factors for algal blooms. However, its accuracy drops with longer prediction periods; as such, the ELM model appears to be more appropriate for chlorophyll-a concentration prediction within 7 d.
The present study has utilized and compared M5P and ELM models to construct data-based chlorophyll-a concentration prediction model, providing foundations for proactive algae management through accurate predictions of occurrence periods and sizes. These results showed ELM can handle more the nonlinearity of algal bloom than M5P. Furthermore, these results lead us to the conclusion that ELM is effective for short-term algal bloom prediction. In future research, we will develop algal blooms prediction model using recurrent neural network and deep neural network.