AbstractChlortetracycline (CTC) is one of the most important compounds in antibiotic production, and its distribution has been widely investigated due to health and ecological concerns. This study presents systematic approach to optimize the high-performance liquid chromatography–tandem mass spectrometry for analyzing CTC in a multiple reaction monitoring mode (479 → 462 m/z). One-factor-at-a-time (OFAT) test with response surface analysis (RSA) was used as optimization strategy. In OFAT tests, the fragmentor voltage, collision energy, and ratio of acetonitrile in the mobile phase were selected as major factors for RSA. The experimental conditions were determined using a composite in cube design (CCD) to maximize the peak area. As a result, the partial cubic model precisely predicted the peak area response with high statistical significance. In the model, the (solvent composition) and (collision energy2) terms were statistically significant at the 0.1 α-level, while the two-way interactions of the independent variables were negligible. By analyzing the model equation, the optimum conditions were derived as 114.9 V, 15.7 eV, and 70.9% for the fragmentor voltage, collision energy, and solvent composition, respectively. The RSA, coupled with the CCD, offered a comprehensive understanding of the peak area that responds to changes in experimental conditions.
1. IntroductionTetracyclines (TCs) have been widely used as antibiotics to treat human infections, in veterinary medicine, and as growth promoters in the livestock industry. TCs including chlortetracycline (CTC), doxycycline (DXC), oxytetracycline (OTC), and tetracycline (TC) have a basic structure comprising a hydronaphthacene backbone containing four fused rings. Various substitutions at the C5, C6, and C7 positions for the backbone characterize different TCs [1–2].
Most antibiotics administered to animals are poorly absorbed in the animal gut after intake, and it is estimated that 25–75% of the antibiotics leave the animals unaltered via feces or urine [3]. It has been suggested that up to 90% of the administered dose of antibiotics may be excreted [4]. Due to the high excretion rate of antibiotics, livestock waste coupled with antibiotic usage can be a potential source of antibiotics in the environment. Wastewater treatment plants (WWTPs) could be another important source of discharged antibiotics because a high percentage of antibiotics are also consumed by humans.
The antibiotic discharge should be considered a serious problem because they can contaminate the aqueous environment, including drinking water supplies. Moreover, long-term exposure to low doses of antibiotics results in selective proliferation of resistant bacteria that transfer antibiotic resistance genes to other bacterial species [5]. Several antibiotic-resistant bacteria and/or genes have been detected in municipal wastewater discharges, surface water, and drinking water [6–7]. Therefore, the occurrence of antibiotics in the environment has been investigated in recent decades. Among TCs, CTC is the most frequently used in cattle, pig, and poultry production [8]. Due to its extensive usage and high adsorption capacity, CTC has been detected in soil, manure, groundwater, sediment, surface water, and municipal wastewater treatment [9–12].
High-performance liquid chromatography–tandem mass spectrometry (HPLC-MS/MS) is commonly used to analyze TCs due to its high sensitivity and specificity [13–16]. However, HPLC-MS/MS sensitivity can change because of variations in operational factors. For example, sensitivity is affected by mobile phase composition, sample volume, injection speed, nebulizer pressure, drying gas conditions of flow rate and temperature, fragmentor voltage, and collision energy. To optimize HPLC-MS/MS sensitivity, selecting the most important variables is necessary to avoid tedious experiments and reduce cost and labor expenditures. Therefore, there is a need to apply a systematic and comprehensive methodology to optimize the HPLC-MS/MS for TC analyses.
In this context, response surface analysis (RSA) is an efficient optimization tool for adjusting the critical operational factors to maximize the dependent variables in complex systems. RSA is a statistical technique that uses multiple regression analysis to build empirical models. It considers the quantitative data obtained from properly designed experiments [17]. The main advantages of optimization via RSA over classical methods, such as one-factor-at-a-time (OFAT) analysis, lies in the large amount of information from a small number of experiments, and observation of interaction effects between independent parameters in the response [18]. Thus, RSA has been used in chemical engineering, bioprocesses, and environmental analysis [19–22]. Particularly in analytical research, RSA is frequently used in the extraction, derivatization, and separation steps [23–25].
Recently, effective CTC analysis has played a critical role in the research fields of degradation, environmental transport and fate, and management policy [12, 26–28]. However, limited information is available on the application of RSA to quantifying procedures in HPLC-MS/MS methods. Therefore, the objectives of this study were to select critical independent variables for analysis of CTC using HPLC-MS/MS, and conduct multivariate regression and optimization using RSA for higher sensitivity.
2. Materials and Methods2.1. Operational conditions of the HPLC-MS/MSCTC hydrochloride (CAS No. 64-72-2) was obtained from Sigma-Aldrich (St. Louis, MO, USA). All chemicals used were of analytical and HPLC grades, and ultrapure water was used in the analysis. The 0.5 mM CTC solution was prepared in methanol and stored at −20°C. The sensitivity was monitored by calculating the peak area according to changes in the operational conditions of the HPLC-MS/MS. CTC analysis was performed using an Agilent 1200 HPLC system (Agilent, Palo Alto, CA, USA) equipped with a reversed phase column (Agilent ZORBAX Eclipse Plus C18, 2.1 × 100 mm I.D., 1.8 μm) (Fig. 1). The mobile phase was composed of 40% A (acetonitrile) and 60% B (0.1% formic acid in water). Addition of formic acid into the mobile phase enhances the sensitivity due to the sufficient amount of proton to promote the desolvation of CTC [29]. The flow rate was 0.2 mL/min with an injection volume of 15 μL. The column temperature was maintained at 25°C using a thermostatically controlled column oven in the HPLC system.
The 6410 Triple Quad Mass Spectrometer (Agilent, Palo Alto, CA, USA) and electrospray ionization (ESI) source in a positive mode interface was operated in multiple reaction monitoring (MRM) mode (Table 1). The CTC transition 479 (M + H+) to 462 m/z was monitored for a dwell time of 200 ms. The fragmentor voltage and collision energy were maintained at 100 V and 15 eV, respectively. The mass spectrometer interface in positive mode was operated under conditions of 4,000 V capillary voltage, 300°C drying gas temperature, 7 L/min drying gas, and 40 psi nebulizer pressure.
2.2. Experimental Design and Response Surface AnalysisThe RSA was used to determine the relationship between peak area at 462 m/z and operational conditions of the HPLC-MS/MS. Sensitivity tests were conducted by changing one factor and fixing the other variables, i.e., OFAT analysis, using the conditions described in Table 1. Then, three factors were selected as independent variables for RSA among the seven operational factors: solvent composition, injection volume, nebulizer pressure, drying gas flow rate, drying gas temperature, fragmentor voltage, and collision energy. The experimental conditions for the RSA were identified based on the central composite in cube design (CCD) using a 3 × 2 orthogonal design [30–31]. The conditions of the center point were fixed as close as possible to the best conditions from the OFAT analysis. The center point was replicated five times to calculate the experimental error. This type of design was used to minimize the number of trials needed to obtain statistically relevant results.
A sequential procedure was conducted as follows: collecting data from the given conditions for the RSA, estimating polynomials (Eq. (1)), and checking the adequacy of the model. For the statistical analysis, Design Expert software (version 6.0.6, Stat-Ease, Minneapolis, MN, USA) was used. The least squares method was used to estimate the parameters in approximating polynomials.
where
3. Results and Discussion3.1. Selection of Major Factors for OptimizationThe peak area of the product ion of CTC, 462 m/z, was tested for the seven factors (Fig. S1). First, solvent composition and injection volume were tested as control factors for the HPLC compartment. The peak area significantly depends on the composition of the acetonitrile in the mobile phase (Fig. S1(a)). The range between 60% and 80% of acetonitrile was optimum. The mechanism for the solvent composition influence on sensitivity is unclear, but a high concentration of acetonitrile in the mobile phase was expected to increase the ionization efficiency by increasing the evaporation capacity of the mobile phase. In Fig. S1(b), the peak area was stable at 2.32 ± 0.40 × 106 disregarding the injection volume in the range of 2–15 μL. Therefore, only acetonitrile concentration was selected for RSA.
Second, the three ionization chamber control factors, i.e., nebulizer pressure, drying gas flow rate, and drying gas temperature, were tested (Figs. S1(c) to S1(e)). The nebulizer pressure regulates the efficiency of the liquid sample spray on the tip of the needle. After spraying, the high temperature and the rapid flow of the drying gas evaporate the water and solvent contents to enhance the ionization of CTC. Among the three factors, only the drying gas flow rate was considered as a major factor for RSA because a dramatic increase in the peak area was observed at a drying gas flow rate of 10 L/min. The drying gas temperature is an important factor to produce desolvated CTC ion, but the temperature range of 250–350°C showed saturated effect on the sensitivity. A previous study also showed that wide range of drying gas temperature, 150–300°C, exhibited the limited effect on the sensitivity of mass spectrometry [32].
Third, the fragmentor voltage and collision energy of the mass spectrometry compartment were tested. These factors are related to the ionization and dissociation of the precursor molecule of 479 m/z. In the sensitivity test shown in Fig. S1(f) for fragmentor voltage, the range between 100 and 150 V was optimum. Generally, a moderate fragmentor voltage in the MRM mode intensifies the ionization of the precursor molecule. However, in this study, a high fragmentor voltage divided the precursor molecule into smaller precursor molecules, including 444 and 462 m/z, rather than of 479 m/z (data not shown). In this case, the peak intensity for 462 m/z obtained in the final detection device was reduced because the first quadrupole only allowed 479 m/z to the next step of the collision induced dissociation (CID) to produce 462 m/z in the MRM mode.
For the best CID, the collision energy should be optimized to generate the 462 m/z product ion by splitting the 479 m/z molecule. An excessively high collision energy splits the 479 m/z molecule into product ions smaller than 462 m/z in the MRM mode, such as 444 and 154 m/z. Using the test presented in Fig. S1(g), 15 eV was identified as the optimum collision energy value for the higher peak area.
The important control factors, including solvent composition, drying gas flow rate, fragmentor voltage, and collision energy, showed significant effects on peak area. Among these factors, the drying gas flow rate was not selected as an independent variable for RSA because the experimental conditions could be optimized by simply increasing the drying gas flow rate. However, the independent variables that showed curvatures in the peak area in the experimental range, such as the solvent composition, fragmentor voltage, and collision energy, were selected as major factors for RSA; varying their values could create different optimum conditions for the HPLC-MS/MS.
3.2. Response Surface Analysis and OptimizationThe list of experimental conditions and corresponding peak areas for RSA are described in Table 2. At the center point, 100 V, 15 eV, and 60% for fragmentor voltage, collision energy, and solvent composition, respectively, were obtained from Section 3.1 as presumed optimum conditions. The drying gas flow rate was increased to 10 L/min, and the other factors remained the same, as in Table 1. The testing ranges for the largest peak area of 462 m/z were chosen as 71.7–128.3 V, 7.9–22.1 eV, and 45.9–74.1% for fragmentor voltage, collision energy, and solvent composition, respectively. An additional trial was undertaken to verify the accuracy of the model prediction by randomly selecting experimental conditions (Trial 16 in Table 2) after obtaining the best model equation that fit the experimental data. The average value of the peak area at the center point was 8.11 ± 0.29 × 106 and the standard deviation was 3.55%.
Initially, a regression with 15 trials, including the center point (Trials 1 to 9 in Table 2), was conducted using a first-order model with least squares to investigate the location of the optimum condition. The step sizes of the variation from the center point were 20 V, 5 eV, and 10% for fragmentor voltage, collision energy, and solvent composition, respectively. The p value for the lack of fit was significant and the regression coefficient for the peak area was not significant at a 5% α-level. Therefore, an additional six trials (Trials 10 to 15 in Table 2) were utilized to find a more appropriate equation to regress the experimental responses at various conditions with a second or higher order model. The step sizes of the variation were expanded to 28.3 V, 7.1 eV, and 14.1% for fragmentor voltage, collision energy, and solvent composition, respectively.
A high R2 value indicates a good explanative power, which is calculated from the ratio of the regression sum of squares to the total sum of squares. In contrast, the adjusted R2 value explains any bias in the R2 value by taking into account the degree of freedom of the independent variables. The R2 and adjusted R2 values for the basic quadratic model (Eq. (2)) were 0.9835 and 0.9650, respectively. The equation was modified to obtain a better quality model, represented by the increased R2 and adjusted R2 values.
where
The addition of the (fragmentor voltage × collision energy2) and (collision energy × solvent composition2) terms to Eq. (2) increased the R2 and adjusted R2 values to 0.9884 and 0.9673, respectively (Eq. (3)). The p value of the regression was significant at a 0.1% α-level and the lack of fit was not significant at a 5% α-level. These results indicated that the partial cubic model was an accurate representation of the data. The residual plots represent the difference between the experimental and calculated values for the model (Fig. S2), and showed no patterns or trends. Therefore, the model described in Eq. (3) was an adequate approximation for the peak area variance according to the variation in fragmentor voltage, collision energy, and solvent composition (Fig. 2).
To find the optimum condition for the largest peak area in the experimental ranges, the response surface of Eq. (3) was analyzed by setting the partial derivatives of the equation to zero with respect to the independent variables. The optimum conditions for the highest response were identified as 114.9 V, 15.7 eV, and 70.9% for fragmentor voltage, collision energy, and solvent composition, respectively, which are near the conditions for Trial 10 in Table 2 (128.3 V, 15 eV, and 60% for fragmentation voltage, collision energy and solvent composition, respectively) where the largest peak area, 8.45 × 106, was observed. The peak area under optimum conditions was estimated as 8.73 × 106. In a separate experiment to verify using triplicate analysis of the expected optimum conditions, the 9.18 ± 0.80 × 106 result showed an insignificant difference from an estimated value of 8.73 × 106, i.e., 5.2%. The predictability of the model obtained in this study was also validated using the randomly selected conditions for Trial 16 in Table 2. There was only a 0.56% error between the predicted value from the model, 6.62 × 106, and observed value, 6.58 × 106. These validations under the optimum and random conditions showed the high accuracy of the model in predicting the response surfaces of the peak area for the target product ion when changing the fragmentor voltage, collision energy, and solvent composition.
A statistical analysis of the independent variables in the model shows that the (solvent composition) and (collision energy2) terms were significant for the peak area at a 0.1% α-level; and (fragmentor) and (solvent composition2) terms were significant for the peak area at a 5% α-level. However, the (fragmentor voltage × collision energy), (fragmentor voltage × solvent composition), (collision energy × solvent composition), (fragmentor voltage × collision energy2), and (collision energy × solvent composition2) two-way interactions were not statistically significant.
In addition to the statistical significance, the coefficient for each term affects the variation in the peak area. To compare the relative effects of terms on peak area, Eq. (3) was converted to Eq. (4), which reflects the normalized step sizes instead of actual values. The normalized step size from the center point is described in Table 2. The largest contribution was attributed to (collision energy2) due to the largest absolute value of the coefficient, 1,857,422. In the same manner, the contributions from terms in Eq. (4) were evaluated. It was considered that interactions had the least influence on the peak area, with rankings of 6 to 10 among the eleven terms. In sum, the interaction between fragmentation voltage, collision energy, and solvent composition had no statistical significance and contribution to variation in the peak area. However, the interaction terms could improve the R2 value, i.e., the predictability of the model.
The sensitivities of individual factors were tested at the optimum conditions. One factor was varied at a time while the other independent variables were fixed. Fig. S3 shows the most significant effect of collision energy among the three independent variables. The significant effect of collision was also expected in Eq. (4), with the largest absolute value of coefficient for (collision energy2). However, the peak area responded with less sensitively to fragmentor voltage and changes in solvent composition.
4. ConclusionsThe HPLC-MS/MS analysis of CTC was optimized using a systematic RSA approach. Before conducting the RSA, important independent variables with significant effects on the sensitivity of the HPLC-MS/MS were selected. Three variables, fragmentor voltage, collision energy, and solvent composition of acetonitrile, were selected as the major factors for optimization due to their significant effects on peak area in the MRM mode (479 → 462 m/z). The peak area data were collected from conditions designed based on the CCD. The RSA of the collected data resulted in an empirical model that precisely predicted the peak area, with R2 and adjusted R2 values of 0.9984 and 0.9673, respectively. The (solvent composition) and (collision energy2) terms were the most statistically significant, while the two-way interactions between independent variables were negligible. The optimum conditions for higher sensitivity of the HPLC-MS/MS were 114.9 V, 15.7 eV, and 70.9% for the fragmentor voltage, collision energy, and solvent composition, respectively. Validation under the optimum and random conditions demonstrated the high accuracy of the model in predicting these results. The applied sequential procedure for screening major factors and conducting RSA provided a rapid optimization and comprehensive understanding of the HPLC-MS/MS for analyzing CTC.
References1. Bruno F, Curini R, Di Corcia A, Nazzari M, Pallagrosi M. An original approach to determining traces of tetracycline antibiotics in milk and eggs by solid-phase extraction and liquid chromatography/mass spectrometry. Rapid Commun Mass Spectrom. 2002;16:1365–1376.
2. Di Corcia A, Nazzari M. Liquid chromatographic–mass spectrometric methods for analyzing antibiotic and antibacterial agents in animal food products. J Chromatogr A. 2002;974:53–89.
3. Elmund GK, Morrison SM, Grant DW, Nevins MP. Role of excreted chlortetracycline in modifying the decomposition process in feedlot waste. Bull Environ Contam Toxicol. 1971;6:129–135.
4. Kroker R. Aspekte zur ausscheidung antimikrobiell wirksamer substanzen nach der chemoterapeutischen behandlung von nutztieren. Wissenschaft Umwelt. 1983;4:305–308.
5. Levy SB. Antibiotic resistance: An ecological imbalance. Ciba Foundation Symposium. 1997;207:1–14.
6. Schwartz T, Kohnen W, Jansen B, Obst U. Detection of antibiotic-resistant bacteria and their resistance genes in wastewater, surface water, and drinking water biofilms. FEMS Microbiol Ecol. 2003;43:325–335.
7. Volkmann H, Schwartz T, Bischoff P, Kirchen S, Obst U. Detection of clinically relevant antibiotic-resistance genes in municipal wastewater using real-time PCR (taqman). J Microbiol Meth. 2004;56:277–286.
8. Daghrir R, Drogui P. Tetracycline antibiotics in the environment: A review. Environ Chem Lett. 2013;11:209–227.
9. Fang H, Han Y, Yin Y, Pan X, Yu Y. Variations in dissipation rate, microbial function and antibiotic resistance due to repeated introductions of manure containing sulfadiazine and chlortetracycline to soil. Chemosphere. 2014;96:51–56.
10. Ma Y, Li M, Wu M, Li Z, Liu X. Occurrences and regional distributions of 20 antibiotics in water bodies during groundwater recharge. Sci Total Environ. 2015;518:498–506.
11. Awad YM, Kim SC, El-Azeem SAA, et al. Veterinary antibiotics contamination in water, sediment, and soil near a swine manure composting facility. Environ Earth Sci. 2014;71:1433–1440.
12. Ashfaq M, Li Y, Wang Y, et al. Occurrence, fate, and mass balance of different classes of pharmaceuticals and personal care products in an anaerobic-anoxic-oxic wastewater treatment plant in Xiamen, China. Water Res. 2017;123:655–667.
13. De Alwis H, Heller DN. Multiclass, multiresidue method for the detection of antibiotic residues in distillers grains by liquid chromatography and ion trap tandem mass spectrometry. J Chromatogr A. 2010;1217:3076–3084.
14. Goto T, Ito Y, Yamada S, Matsumoto H, Oka H. High-throughput analysis of tetracycline and penicillin antibiotics in animal tissues using electrospray tandem mass spectrometry with selected reaction monitoring transition. J Chromatogr A. 2005;1100:193–199.
15. Hirsch R, Ternes TA, Haberer K, Mehlich A, Ballwanz F, Kratz K. Determination of antibiotics in different water compartments via liquid chromatography–electrospray tandem mass spectrometry. J Chromatogr A. 1998;815:213–223.
16. Zhu J, Snow DD, Cassada DA, Monson SJ, Spalding RF. Analysis of oxytetracycline, tetracycline, and chlortetracycline in water using solid-phase extraction and liquid chromatography–tandem mass spectrometry. J Chromatogr A. 2001;928:177–186.
17. Montgomery DC. Design and analysis of experiments. 3rd edNew York: Wiley; 1991.
18. Shokuhfar A, Khalili SMR, Ghasemi FA, Malekzadeh K, Raissi S. Analysis and optimization of smart hybrid composite plates subjected to low-velocity impact using the response surface methodology (RSM). Thin-Walled Struct. 2008;46:1204–1212.
19. Zhou Y, Song J, Choi FF, et al. An experimental design approach using response surface techniques to obtain optimal liquid chromatography and mass spectrometry conditions to determine the alkaloids in Meconopsi species. J Chromatogr A. 2009;1216:7013–7023.
20. Arslan-Alaton I, Ayten N, Olmez-Hanci T. Photo-Fenton-like treatment of the commercially important H-acid: Process optimization by factorial design and effects of photocatalytic treatment on activated sludge inhibition. Appl Catal B Environ. 2010;96:208–217.
21. Chauhan B, Gupta R. Application of statistical experimental design for optimization of alkaline protease production from Bacillus sp. RGR-14. Process Biochem. 2004;39:2115–2122.
22. Gopinath KP, Muthukumar K, Velan M. Sonochemical degradation of Congo red: Optimization through response surface methodology. Chem Eng J. 2010;157:427–433.
23. Ferreira SLC, Bruns RE, da Silva EGP, et al. Statistical designs and response surface techniques for the optimization of chromatographic systems. J Chromatogr A. 2007;1158:2–14.
24. Fang Y, Tian W, Pei F, et al. Simultaneous determination of pesticide residues and antioxidants in blended oil using a liquid-liquid extraction combined with dispersive solid phase extraction method. Food Chem. 2017;229:347–353.
25. Fan S, Zhu J, Ren L, et al. Co-solvent enhanced adsorption with magnetic velvet-like carbon nitride for high efficiency solid phase extraction. Anal Chim Acta. 2017;960:63–71.
26. Salazar-Rábago JJ, Sánchez-Polo M, Rivera-Utrilla J, Leyva-Ramos R, Ocampo-Pérez R. Role of 1 [O2]* in chlortetracycline degradation by solar radiation assisted by ruthenium metal complexes. Chem Eng J. 2016;284:896–904.
27. Raghavan DSS, Qiu G, Ting YP. Fate and removal of selected antibiotics in an osmotic membrane bioreactor. Chem Eng J. 2018;334:198–205.
28. Di Guardo A, Finizio A. Sustainable use of veterinary pharmaceuticals on the territory (Sust-PHarm): Linking available database of manure management and environmental fate models. Sci Total Environ. 2017;575:1014–1026.
29. Shao B, Jia X, Zhang J, et al. Multi-residual analysis of 16 β-agonists in pig liver, kidney and muscle by ultra performance liquid chromatography tandem mass spectrometry. Food Chem. 2009;114:1115–1121.
30. Bae H, Paul T, Kim D, Jung JY. Specific ANAMMOX activity (SAA) in a sequencing batch reactor: Optimization test with statistical comparison. Environ Earth Sci. 2016;75:1452–1460.
Fig. 1Schematic diagram of the HPLC-MS/MS system. The operational factors for the sensitivity test are highlighted. 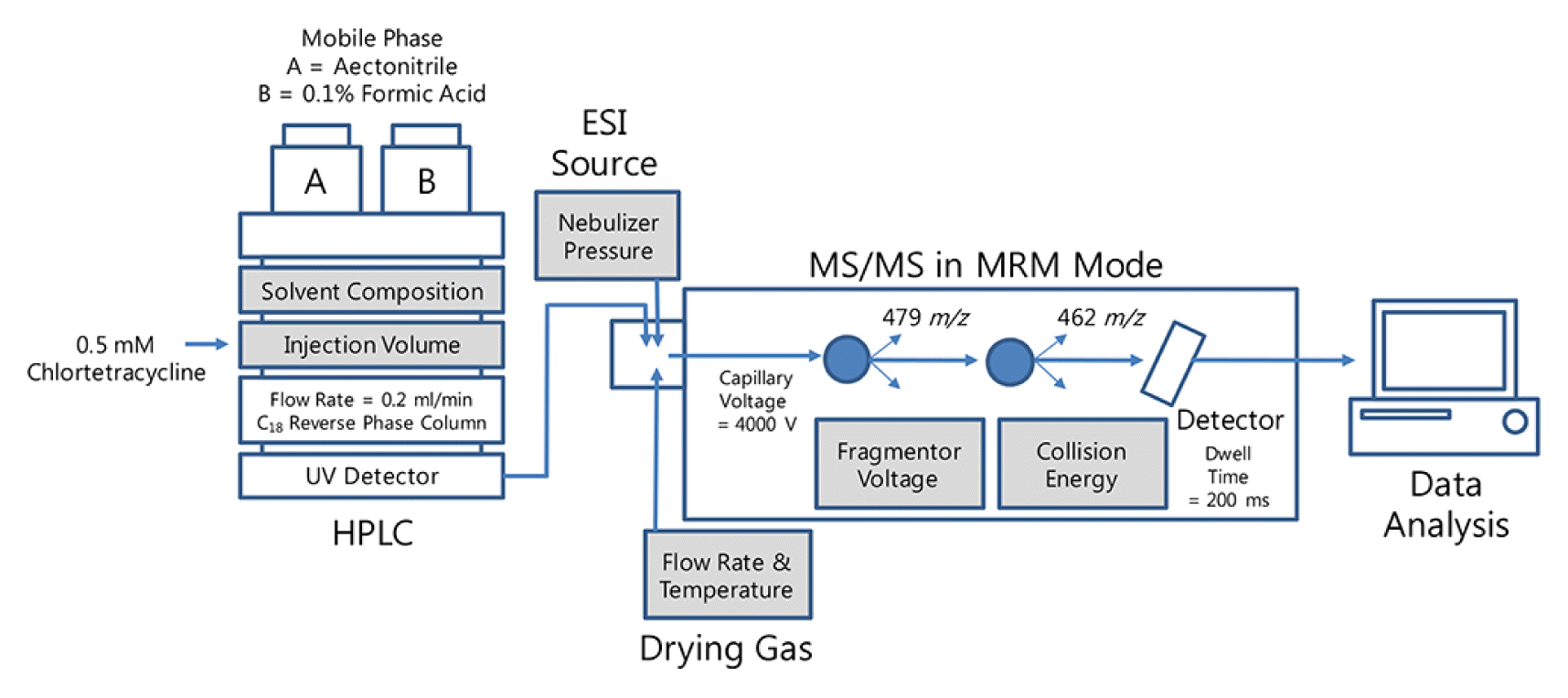
Fig. 2Three-dimensional contour plots of the partial cubic model for the peak area for the (a) fragmentor voltage and collision energy, (b) collision energy and solvent composition, and (c) fragmentor voltage and solvent composition. 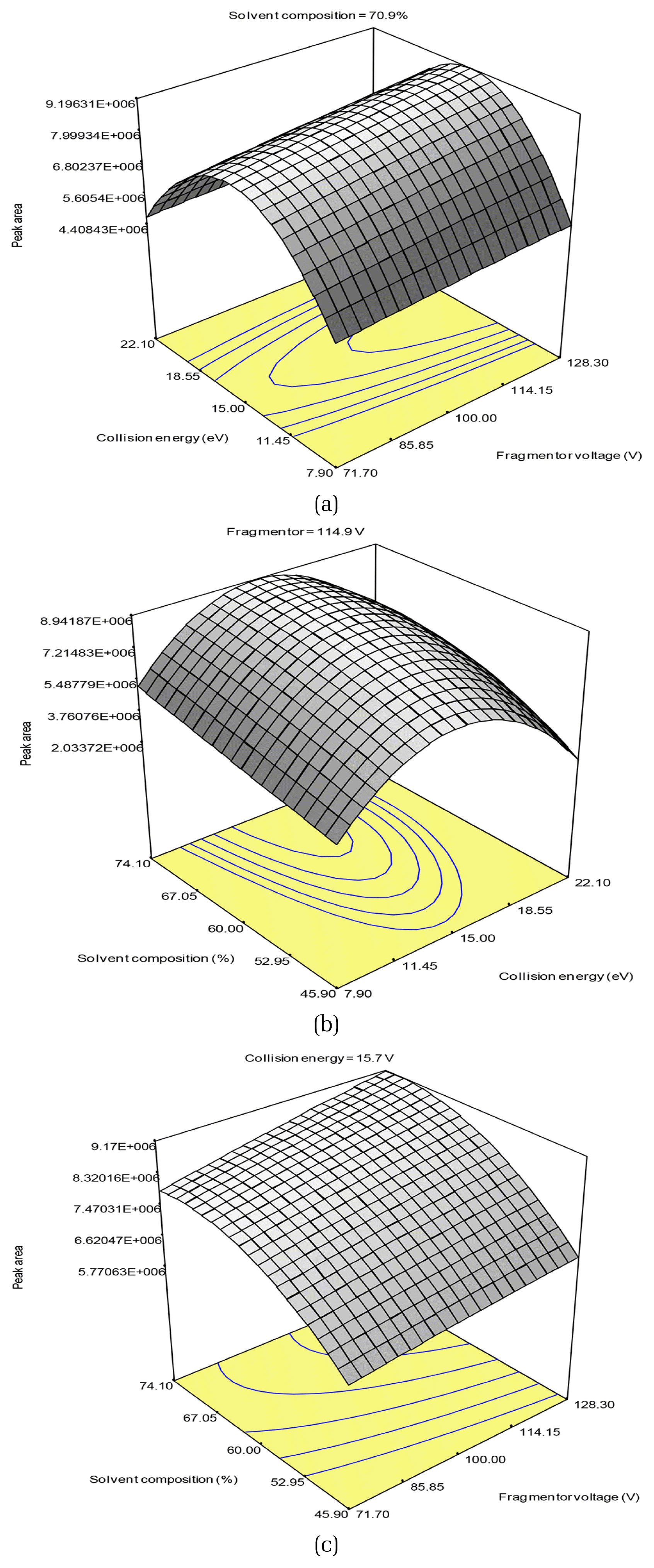
Table 1HPLC-MS/MS Operational Conditions for the Sensitivity Test Table 2Experimental Design for Optimizing the HPLC-MS/MS and Observed Peak Areas
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||