1. Introduction
The phosphogypsum (PG) is a solid byproduct generated by the manufacture of phosphate fertilizers during the production of phosphoric acid [1]. The PG is composed of hydrated calcium sulfate mixed with some impurities such as P2O5, fluorine, organic matter, heavy metals and radioactive elements [2, 3]. For each ton of produced phosphoric acid, five tons of PG is generated [4]. The worldwide production of PG quantities is between 100 and 280 million tons per year [5, 6], which induces environmental threats and available storage areas problems [7]. Generally, the PG is dumped in the vicinity of the production plants in large stockpiles causing atmospheric pollution and contamination of groundwater, superficial water and soils [8–11]. Therefore, a strict policy is deemed to be an essential measure to limit pollution and encourage the valorization of PG [12]. Actually, the worldwide reuse of PG is only 15% of the total PG produced [13], in some applications as plaster manufacturing, cement production [14–18], roadway construction [19], agriculture [20], solid brick and raw building block [21, 22].
The PG purification techniques can be divided into three different types: physical, thermal and chemical. The physical treatments were based on the particle size separation while the thermal one consisted of heating the PG at different temperatures [14]. The PG chemical treatment includes mixing with aqueous ammonium hydroxide solution and aqueous citric acid solution [23]. Also, the PG treatment with a mixture of sulfuric acid and silica or hot aqueous ammonium sulphate permitted to get rid of the impurities [14].
Although such treatments produce a good purified PG quality, which can substitute the natural gypsum, but the treatment of PG using sulfuric acid solutions remain preferred in the industry due to its availability in the phosphoric acid plants [24].
Several researchers noted the effectiveness of the PG treatment using sulfuric acid. Jarosinski et al. [25] adapted a method of leaching PG with dilute sulfuric acid solution to recover rare earth elements, followed by production of anhydrite from the purified PG by recrystallisation in concentrated sulfuric acid solution. The results have shown that the undesirable impurities were considerably reduced and the obtained anhydrite can be used for plaster production. Van Der Merwe and Strydom [26] and Lokshin et al. [27, 28] have described a method to purify PG by a dilute sulfuric acid treatment or by a combined thermal and sulfuric acid treatment. A significant amount of impurities was successfully removed by these treatments and the treated PG can substitute natural gypsum in Portland cement. Aliedel et al [29] used a full factorial methodology (considering four factors) to optimize PG purification process using sulfuric and nitric acid solutions.
Hammas-Nasri et al [24] performed a purification process for concentrating rare earth elements from Tunisian PG on a double leaching of PG with diluted sulfuric acid at 60°C.
According to the most researches, temperature, sulfuric acid concentration, solid /liquid ratio and stirring time were the most frequently operating parameters affecting the PG purification process [25–26, 29–30].
In most studies, these factors are analyzed independently which may lead to an under estimate of their combined effect. Hence, to overcome this problem, a methodology based on the study of the main effects and the interactions between operating variables using the full factorial design methodology is considered [31].
In the current study, a purification process of PG was developed. The latter is composed of four steps, namely mixture of PG with dilute sulfuric acid solution, floatation, filtration and washing. The three most important experimental factors in different ranges affecting the purification process of PG are temperature, the volume of aqueous sulfuric acid solution and the quantity of PG. In order to adjust the purification process, a full factorial design (FFD) methodology was applied to test the significance of factors and their relative interaction [32, 33]. Regression models were also applied in order to best represent factors interactions through their best fit to the experimental data [34]. Recently, several researchers have used regression models in several fields, such as forecasting the inflow of a dam reservoir by using Auto Regressive Moving Average (ARMA) and Auto Regressive Integrated Moving Average (ARIMA) models and comparing them with the static and dynamic artificial neural networks [35]. Regression models are also used to assess radiation –based models versus the FAO Penman- Monteith (FPM) model to determine the best model under different climatic conditions [36] and to study the effect of the length of recorded data to achieve reliable accuracy for monthly rainfall estimations [37]. Moreover, regression models were applied to irrigation management under different scenarios [38], to estimate the area equipped for irrigation under different scenarios [39] and to estimate the potential evapotranspiration (ET0) in Arid, Semiarid, Mediterranean and very humid climates considering climate change and magnitudes of extreme events [40].
A regression model is presented for the response variable: % P2O5, % F, Total Organic Carbon (TOC) (mg.kg−1) and pH as a function of temperature, volume of aqueous sulfuric acid solution and the quantity of PG. A statistical approach based on response surface methodology (RSM) was used to optimize operating conditions in the process of purification.
The ranges of operating factors were chosen by considering literature data on the PG purification using sulfuric acid solution. According to the most reported studies, the optimum concentration of sulfuric acid solution is 5% [25, 26]. The contact time and agitation speed were chosen of 30 min and 150 rpm, respectively based on the previous study [26, 29, 30].
A temperature of 30°C which is the most usually used was chosen as the minimum level in our study whiles the highest one was selected as 60°C [24–27]. The solid /liquid ratio has been studied in the range of 1:1 to 1:4 [25, 26, 30]. The maximum volume of sulfuric solution in the present case was set to 3 L while the minimum one is 1 L. The range of PG quantity, chosen based on previous studies, is 1 to 2 kg [28, 30].
However, none of the previous reports investigated the combined effect of temperature, volume of aqueous sulfuric acid solution and the quantity of PG on the PG purification process nor evaluated the decrease of the impurities that could be obtained under optimal process conditions. The novelty of this investigation was to use a full factorial design of the experimental program in order to study the effects of the process variables at different levels as well as their interactions. Moreover, the RSM was applied in this study to define optimal condition for the PG purification process with the aim of practical application of the process and not only the technical feasibility. The purified PG obtained under optimal conditions was characterized by chemical analysis, pH and radioactivity measurements. The purified PG was calcined to produce plaster. The physical properties of the final product were also discussed.
2. Materials and Methods
The PG samples used in this study were obtained from the PG stockpile at Sfax city, Tunisia. The average chemical composition of the PG samples is given in Table 1. The PG is mostly (about 94.8%) made up of calcium sulfate dihydrate (CaSO4.2H2O) or gypsum. The remaining components, expected SiO2 (3.76%), are present at low percentages (P2O5 (1.54%), F (1.3%), TOC (0.7%) and Na2O + K2O (0.3%)). It should be noted that the pH of PG samples is around 3.9, indicating the high acidity of the PG.
2.1. Purification of Phosphogypsum
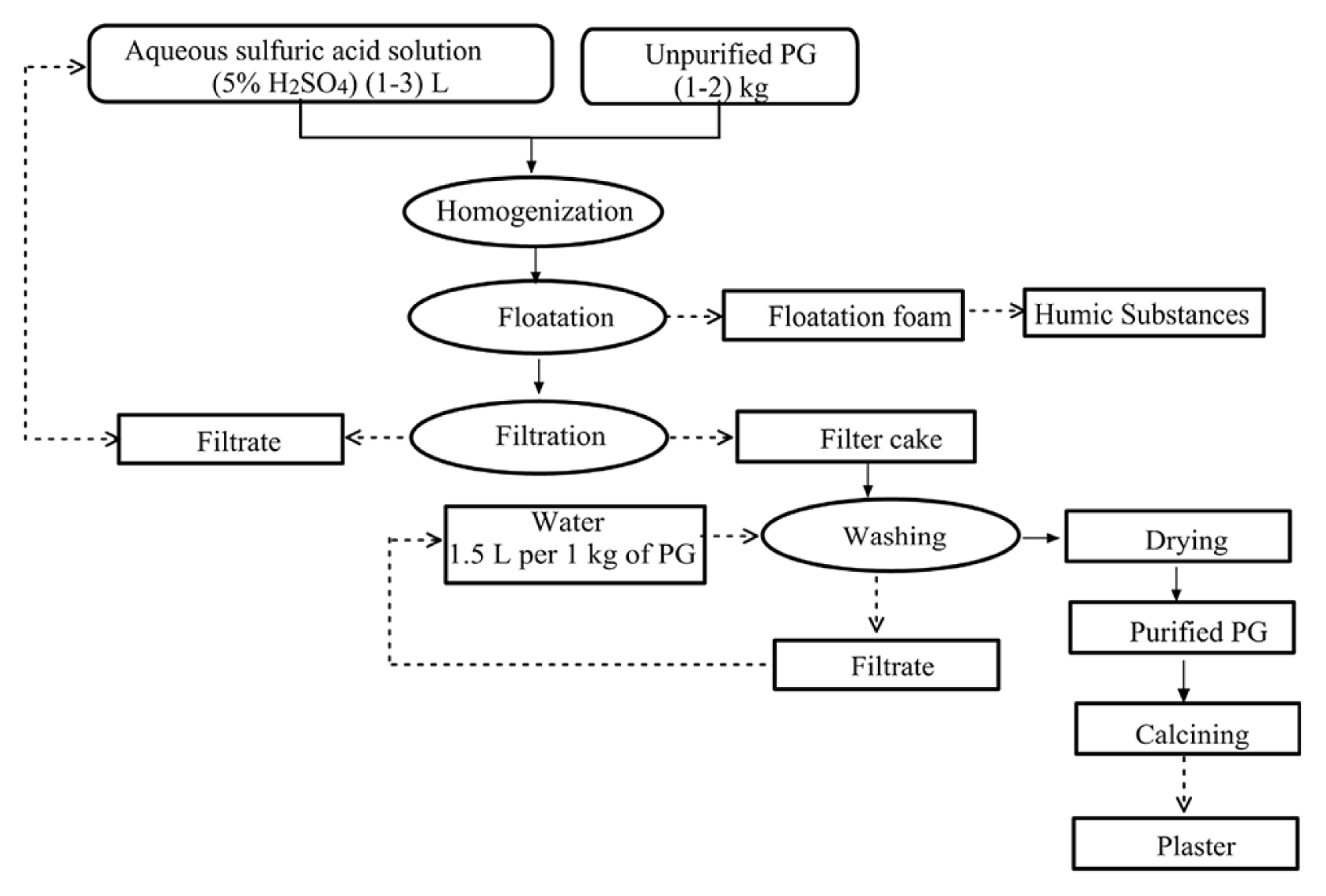
The purification experiments were conducted in a stirred tank reactor of 10 L volume, which was immersed in a thermostatic bath to keep the temperature constant throughout the reaction. The reactor was loaded with a quantity of PG and a volume of aqueous sulfuric acid solution (5% H2SO4). The experiments were carried out for solution temperatures of 30°C and 60°C. The stirring was set at 150 rpm for 30 min. The solution was floated for 30 to 45 min using a floatation cell. The foam of floatation is formed of humic substances already present in the PG. Then, the pulp was filtered through a funnel, washed with water (1.5 L per 1 kg of PG) and dried 24 h at 65°C (Fig. 1).
2.2. Radioactivity Measurements
Activity concentrations of 226Ra, 228Ac, 232Th, 40K and 212Pb were measured in samples of PG using a typical non–destructive nuclear technique at the INSTN laboratory of the National Institute of Nuclear Science and Technology, Tunisia. This analysis was performed using ɣ-ray spectrometer equipped with a high pure germanium detector coaxial p-type HPGe with 80% relative efficiency. Samples were packed in 100 cm3 cans and sealed for about one month to ensure equilibrium between 226Ra and its daughter products, before being taken for gamma-ray spectrometric analysis. The 226Ra activities were determined by taking the mean activity of three separate photo peaks of its daughter nuclides: 214Pb at 295 and 352 keV, and 214Bi at 609 keV.
The 232Th content was determined by measuring the intensities of the 911 and 968 keV gamma-ray peaks from 228Ac. The potassium content was determined from the 1,460 keV gamma-ray peak of 40K. The concentration of 212Pb was determined from the 239 keV gamma-ray peak.
2.3. Full Factorial Design
The three factors investigated in this study were temperature (factor X1); volume of aqueous sulfuric acid solution (factor X2), and PG quantity (factor X3). The influence of these factors variations on the responses of the % P2O5 (Y1), % F(Y2), TOC (mg.kg−1) (Y3) and pH(Y4) was evaluated using a 23 FFD. A total of 8 experimental runs were performed. The range limits for each factor were assigned the values of (−1) and (+1), respectively (Table 2). The X1 factor varied between 30 and 60°C, the X2 between 1 and 3 L and X3 between 1 and 2 kg [41].
The responses of the experimental design were investigated using Statgraphics Centurion XVI software [42]. The analysis was performed through the plotting of Pareto charts and response surface and the analysis of the variance. The design matrix, presented in Table 3, shows 8 experiments issued from combinations of Xi factors variations and their corresponding responses Yi.
The regression equation based on the first-order model with three operating variables and their interaction terms are given by the following expression:
3. Results and Discussion
The aim of the FFD was to find the significant factors on the process and the optimum set of their values to fix the process results on the preferred conditions. The design of the FFD for three control factors using the Statgraphics Centurion XVI software is presented in Table 3 for the 8 experiments responses of the process % P2O5, % F, TOC (mg.kg−1) and pH.
3.1. Model Fitting and Statistical Analysis
The purification experiments were conducted in a random order to determine the effect of the factors on four characteristic responses: % P2O5, % F, TOC (mg.kg−1) and pH. The Analysis of the Variance (ANOVA) was performed to determine the statistical significance of factors. The results of ANOVA for the four responses are listed in Table 4 where the p-value is the probability value used to determine the significant effects in the model. The effect was statistically significant for p-value less than 0.05 when a 95% confidence level is considered [45]. Our results indicate that for Y1, Y2 and Y4, X2 was the most significant factor followed by X3 then X1. However, for the Y3, X2 was also the most significant factor followed by X1 then X3. The analysis revealed that X2–X3 interaction has significant effect on Y2, Y3 and Y4. Moreover, X1–X3 interaction has a significant effect on Y1, Y3 and Y4. Finally, X1–X2 interaction has significant effect on Y4. The relative importance of the main effects and their interactions was also studied using standardized main effect Pareto charts (Fig. 2). Each factor exceeding the vertical line is considered as statistically significant [46]. The % P2O5 was found to be directly proportional to the temperature (X1) and the interaction of X1–X2, while indirectly proportional to the volume of solution (X2) and quantity of PG (X3) as shown in Fig. 2(a). The temperature, volume of solution and the interaction X2–X3 have a strong negative effect on % F (Fig. 2(b)). The Pareto Chart of Fig. 2(c) for the TOC (mg.kg−1) shows that with the increase of the temperature and volume of solution the TOC decreases. Moreover, the interaction X2–X3 has a strong negative effect on the reduction of the TOC. However, the interaction X1–X3 has a strong positive effect on the reduction of the TOC. Actually, the pH is found to be directly proportional to the temperature (X1), the volume of solution (X2) and the interactions X1–X2, X2–X3 and X1–X3, while indirectly proportional to the quantity of PG (Fig. 2(d)).
After the elimination of insignificant parameters (p-value > 0.05) in Table 4, the final empirical models based on Eq. (1) at 95% confidence level can be represented as:
Removing the insignificant terms from the full model has produced the final models for each response that is more effective as a predictor of new data.
3.2. Model Adequacy Checking
The statistics used to test the adequacy of the models at confidence level of 95% are summarized in Table 5. The coefficient of determination (R2) evaluates the model suitability. It is accepted that for a good fit model, R2 should be in the range from 0.80 to 1. However, the use of adjusted R-squared (Adj-R2) is preferred to evaluate the model adequacy because it is adjusted for the number of factors in the model. The Adj-R2 may decrease if insignificant factors are added to the model. The regression model explains well the process when Adj-R2 is higher than 0.90 [47]. All the statistics given in Table 5 indicate that the estimated model for each response fits the experimental data adequately as the R2 varied between 0.98 and 0.99 and the Adj-R2 between 0.95 and 0.99.
3.3. Three-dimensional Response Surface Plots
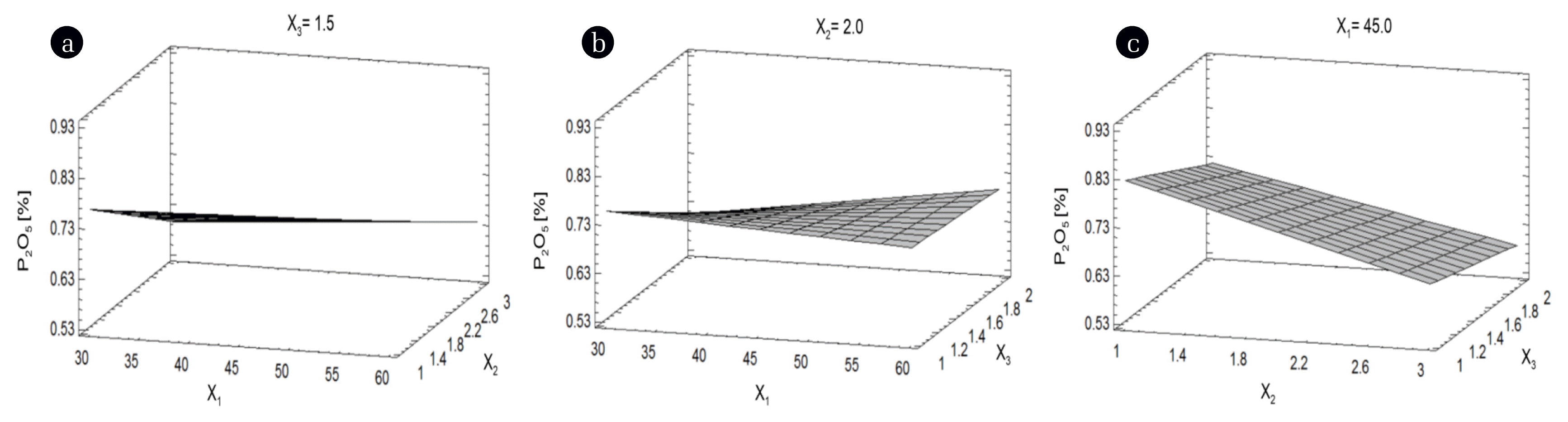
Three-dimensional (3D) plots represent the simultaneous effect of any two factors on the response parameter, at a constant level of the third factor [48]. The temperature (X1) and the quantity of PG (X3) did not significantly decrease the % P2O5 (Figs. 3(a) and (b)). However, the % P2O5 decreased when the volume of solution (X2) increased (Figs. 3(a) and (c)). The % P2O5 became lower when the temperature (X1) was kept on the level of −1 (30°C) (Figs. 3(a) and (b)). The lower % P2O5 was achieved at a higher volume of solution (X2) and at lower quantity of PG (X3) (Fig. 3(c)).
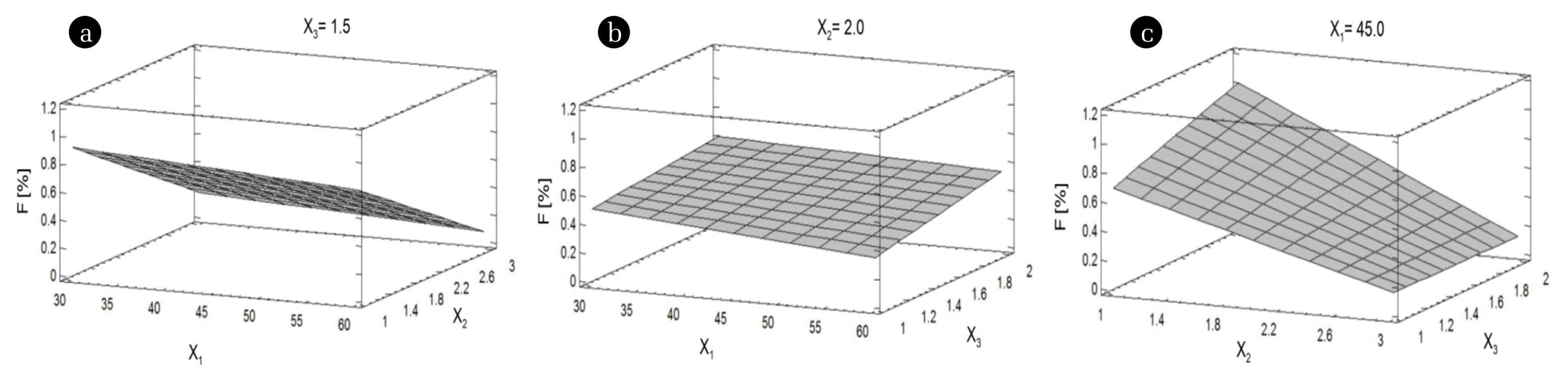
The % F decreased when the temperature (X1) and the volume of solution (X2) were increased (Fig. 4(a)). The increase of the PG quantity (X3) caused an increase in % F, which might be due to the addition of more PG, especially impurities that need to be eliminated (Fig. 4(b)). The lower % F was acquired at a higher volume of solution (X2) and at lower quantity of PG (X3) (Fig. 4(c)).
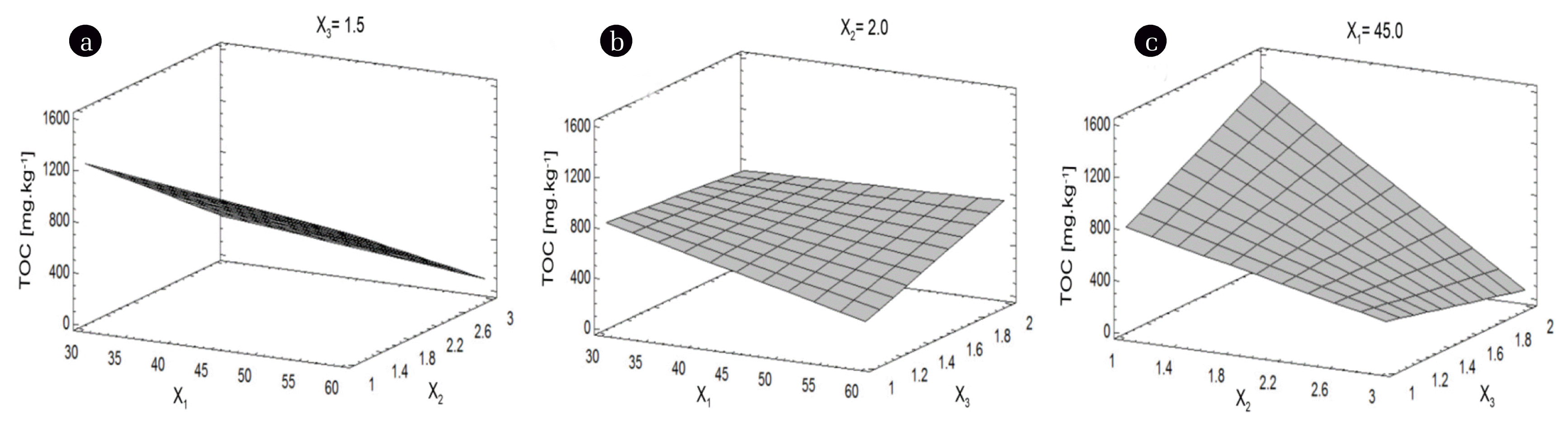
The increase of the solution volume (X2) caused the decrease in the TOC (Fig. 5(a) and (c)) and the increase in the PG quantity (X3), in turn, caused the increase in the TOC due to the addition of more organic matter (Fig. 5(b)). The TOC became lower when the temperature (X1) was kept on level +1 (60°C) (Figs. 5(a) and (b)) and the abutment TOC was observed at higher volume of solution (X2) and lower quantity of PG (X3). The effect of solution volume (X2) is the greatest one (Fig. 5(c)).
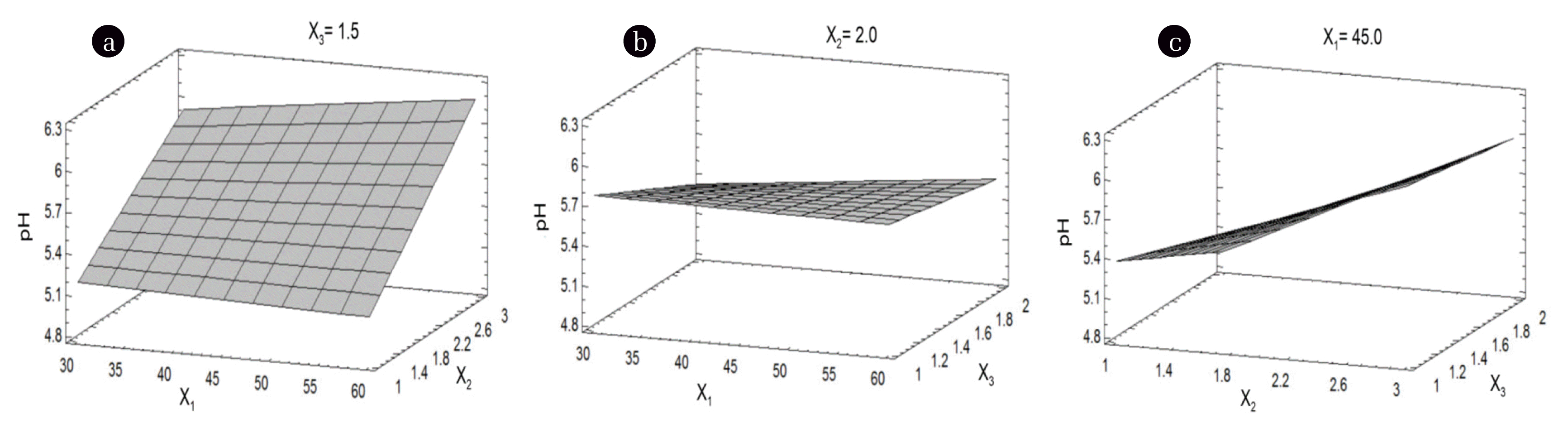
It is to be noted that the pH increased when the solution volume (X2) was increased. This positive effect could be probably related to the solubility of impurities in the aqueous sulfuric acid solution such as P2O5. The temperature (X1) and the quantity of PG did not significantly increase the pH (Figs. 6(a) and (b)). At the highest volume of solution (X2), the pH increased with the increase in temperature (X1). The higher pH was achieved at the higher volume of solution (X2) and lower quantity of PG (X3) (Fig. 6(c)).
3.4. Optimization of Process Parameters and Experimental Verification
The aim of operating factors optimization, using FFD is to improve the purification process. The multi-response method named desirability function (DF) was applied for this purpose. This approach allows the combination of multiple responses into one response (DF) by the choice of a value between 0 to 1.
This method comprises the following steps. First, for each response (Yi), a desirability score (di) is assigned by an appropriate function. Second, all individual desirability scores are combined on an overall desirability function (DF), which is optimized to find the optimum set of parameters [49]. At the best point with maximum overall desirability of 0.9, the optimum temperature, volume of solution and quantity of PG were found to be 60°C, 3 L and 1 kg, respectively. Under the optimum conditions, the predicted values of P2O5, fluorine, TOC and pH were 0.64 (%), 0.07 (%), 108 ppm and 6.2, respectively. If compared to experimental values performed at optimized operating conditions of 0.64 (%), 0.1 (%), 87 ppm and 6.2, respectively (Table 6), the model predicted ones were approximately similar at the statistical significance level of p < 0.05, which induce an approving of the good prediction of the model.
Under these operating conditions, a mass balance was calculated and used for the verification of technical feasibility of the process. In the purification process, approximately 3 liters of diluted sulfuric acid solution are used for treating one kilogram of PG, containing 9.6% of free water. After filtration, approximately 3.6 liters are recovered and recycled in the purification process (Fig. 1). The 0.92 kilograms of obtained PG after purification, containing 20% free water, was dried at a temperature of 65°C. Accordingly, the mass balance indicates that 81.4% of the brut PG went into the production of plaster and the rest went with the fine wastes.
3.5. Characteristics of the Purified PG
To investigate the performance of the purification process under optimum conditions, the main chemical components P2O5, F, TOC, Na2O + K2O and the pH of the PG before and after purification are presented in Table 7. It can be seen that the purified PG complies with the requirements given in IS: 12679–1989, specification for gypsum use in plaster, blocks and boards [50].
The PG contents of heavy metals were analyzed using ICP spectroscopy before and after purification and given in Table 8. The maximum drop was observed for Cd and Zn passed from 15 to 2 mg. kg−1 and from 100 to 14 mg. kg−1, respectively. The concentration of metals is comparable to that of the natural gypsum and well below the regulatory limits in Ajam (2010) [51], which justify the performance of the purification.
Several studies have reported that the radionuclide activity levels in the PG were concentrated in the fine fraction and were constituted a small percentage of the PG [52]. In the first step of PG purifying, a dilute acid is used to digest the PG. The pulp is shacked for a sufficient period. After that, during the floatation step the fine particles containing radioelements are removed. Then, the pulp is filtered and the remaining radio-elements are removed by the filtration step.
The activity concentration values of the radionuclides in PG samples before and after purification are summarized in Table 9. Hence, about 12.2, 36.5, 48.2 and 36.5% of Ra-226, Ac-228, Pb-212 and Th-232, respectively, were successfully removed from the PG. The purified PG content of radionuclide elements (226Ra, 228Ac, 232Th, 40K and 212Pb) are below the limits fixed by the standards [53].
The analytical results showed a better removal of P2O5 than that obtained by Van Der Merwe and Strydom [26] for stirring PG in sulfuric acid (5%) for 30 min at ambient temperature and a solid/liquid ratio of 1:4. Also, these values are higher than reported by Jarosinski et al [25] for the removal of Fluor from PG by treating PG with a 10% sulfuric acid solution.
3.6. Production of Plaster from Purified PG
After purification of PG under optimum conditions, the reduction of impurities conformed with the requirement as given in IS: 12679–1989, specification for byproduct gypsum for using plaster blocks and board. The Gypsum plaster (CaSO4. 1/2H2O) was produced by calcining purified PG at 130–170°C for 4 h. The plaster was tested for various physical properties according to the French Standard EN 13279-2 (Part 2) [54]. The comparative physical properties (consistency, setting time, compressive strength and expansion) of the obtained gypsum plaster from natural gypsum and the purified PG are given in Table 10. The plaster produced with purified PG was found to have similar physical properties to those produced from natural gypsum and conform to the French standard EN 13279-1 specifications [55]. This proved the efficiency of the purification methodology to remove the impurities to a large extent. The plaster produced with purified PG was found to have a higher consistency than that obtained from natural gypsum. This was due to the fine size distribution of PG. Hence, the gypsum plaster can be used for building products like boards, blocks, bricks and a variety of cement binders.
4. Conclusions
The accumulation of PG causes environmental threats and storage problems. In order to valorize the huge accumulated quantities, several processes are used to remove impurities. These processes are based specially on the treatment of PG using sulfuric acid solutions. However, these studies have reported that the temperature, the volume of aqueous sulfuric acid solution and the quantity of PG were the most examined factors affecting the PG purification. There is no example in the literature helps to understand how these factors influence the purification process. Also, no research can determine and statistically evaluate the interrelationship among the process factors. In the present research work, an experimental process using diluted sulfuric acid was developed and optimized to purify the PG. A 23 full factorial design methodology was used to evaluate the main effects and interaction effects of temperature, volume of aqueous sulfuric acid solution and PG quantity. The %P2O5, %F, TOC (mg.kg−1) and pH were selected as the response variables of the model design. The factorial design results showed that the optimum conditions of temperature, volume of aqueous sulfuric acid solution and PG quantity were found to be 60°C, 3 L and 1 kg, respectively. The process of purification was performed under optimum conditions, the impurities (P2O5, F, and TOC) decreased and the pH increased. The analysis by ICP has proven that the major toxic impurities are reduced after purification. Under the optimum conditions, the predicted values of P2O5, fluorine, TOC and pH were validated by comparison to experimental values and a statistically high level of similarity is recognized. The purified PG can produce gypsum plaster (CaSO4.1/2H2O) of improved setting and strength characteristics. The plaster can be used as building materials.