1. Introduction
While a water quality model with higher complexity may provide more detailed or accurate prediction results, it is prone to provide increased uncertainty due to greater chance of error propagation [1]. Also, inappropriate integration step size in either temporal or spatial scale may result in errors due to numerical dispersion of numerical methods [2] and thus can make model results less reliable. Seo and Kim [3] and Seo et al. [4] reported that it required few days to few weeks for annual water quality modelling of the Nakdong River in Korea using combination of 3-dimensional EFDC hydrodynamics model [5] and WASP water quality model [6, 7] and this could be prohibitive to use for intensive scenario analysis or statistical analysis. While many researchers reported that a smaller grid size is preferred for more accurate prediction for their modelling applications [8–11], it seems many other researchers arbitrarily select grid resolutions without sufficient consideration on grid size determinations [12, 13]. Seo [14] compared a different number of cells when using a combination of EFDC and WASP model to calibrate the thermal stratification of Lake Yongdam, Korea. Kim [3] confirmed that detailed resolution was necessary by increasing number of vertical layers to accurately model thermal stratification of Lake Yongdam, Korea.
There have been many researches on effect of grid size especially for hydrological study using GIS data [15–17]. However there have not been many practical studies on how to select the optimum grid size for water quality modelling especially when used with hydrodynamics model. In this study, methods to determine the optimum number of grid size for accurate and efficient water quality modelling applications was analysed and discussed. Salinity was chosen as a surrogate of water quality contaminant and an artificial canal was chosen as a test study site.
2. Materials and Methods
2.1. Study Area
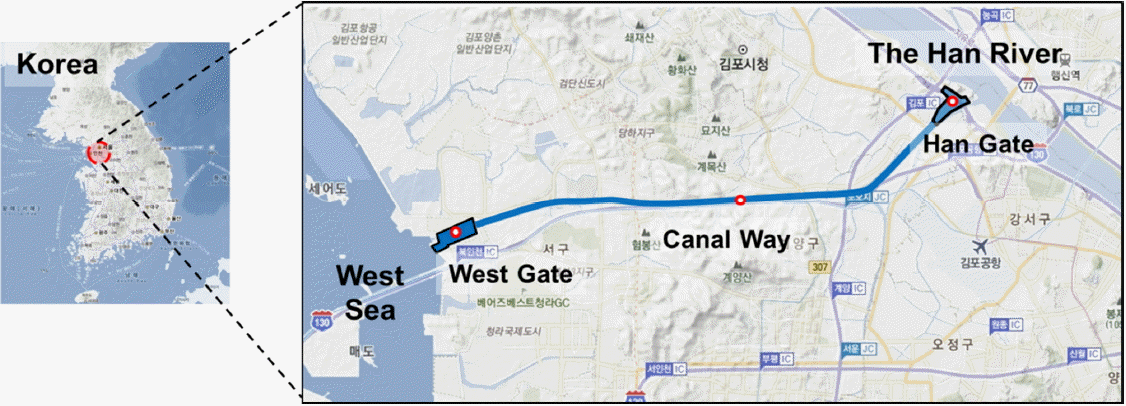
For this study an artificial canal constructed recently in Korea chosen as a test site. Data shown here may not be accurate and thus can be regarded as data for reference purpose due to limited availability of information of the construction. The Ara Canal was constructed to prevent flood damages in the Goolpocheon River basin and also to promote economic development of the area by reducing logistic costs. The canal is connecting the Han River that passes through Seoul City and the western coastal area of Korea (Fig. 1). There are two gates at both ends of the canal. The canal gate in the Han River side is located near Haengju Bridge at a downstream area of the river. The other gate in the ocean side is located in Incheon City facing western costal area of Korea. The canal is 18 km long overall while the navigation channel length is 15.6 km. The width of the navigation channel is 80 m and the average water depth is 6.3 m. Table 1 shows the general information of the Ara Canal [18].
Mixing of freshwater from the Han River and salt water from the coastal area with frequent gate operation for navigations may create complicated salinity distribution due to density differences between salt water and fresh water.
This hydrodynamic behaviour inside the canal will affect water quality kinetics including the growth of phytoplankton and dissolved oxygen depletion. To consider both water quantity and water quality issues during gate operations, it is suggested to use an advanced hydrodynamic and water quality model.
2.2. The EFDC (Environmental Fluid Dynamics Code) Model
The Environmental Fluid Dynamics Code (here after EFDC) model and has been used widely for hydrodynamic and water quality modeling in rivers, lakes, estuaries and coastal systems [5]. Grid development of the EFDC model for the study site is as shown in Fig. 2. Wool applied a combination of hydrodynamic module of EFDC and the WASP water quality model for modeling of the Neuse River including its estuarine area [7]. Seo [4, 19] and Kim [4] also used the EFDC-WASP combination to model major rivers in Korea. Jung compared a 2-dimensional SMS model [20] and 3-dimensional EFDC model to predict salt intrusion in the Sumjin River, Korea and reported that the EFDC model showed more accurate results [21]. Noh analyzed the effect of flushing discharge on salt water intrusion in the Sumjin River estuarine area using EFDC model [22]. The detailed theoretical background and explanation of the model can be found in EFDC manuals [23].
2.3. Input Development of the EFDC Model
2.3.1. Initial grid
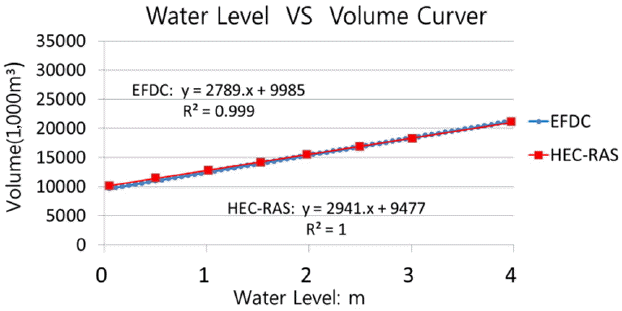
Morphological information of the area was obtained from their environmental impact assessment report of the study area [18]. Information about in-stream structures and the grid system for HEC-RAS [24] model were used to develop grid systems for EFDC application in this study. Fig. 3 compares water level versus the volume curve of the canal from the HEC-RAS model of the previous study and the EFDC model in this study. Two model results are almost identical and this shows that the EFDC grid in this study reflects the physical characteristics of the canal appropriately.
2.3.2. Boundary conditions
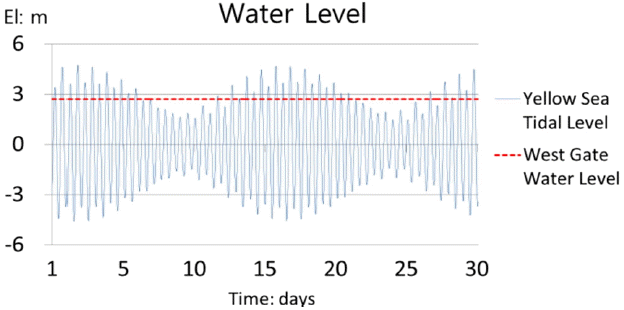
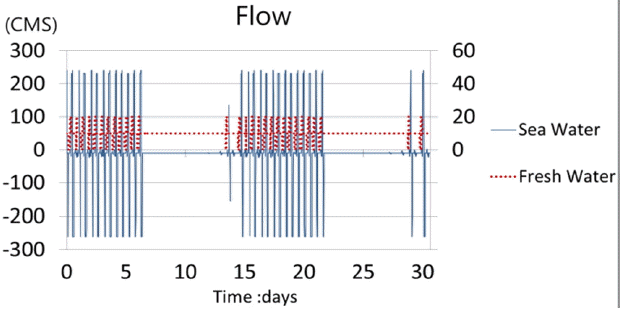
Inflow for the west gate of the canal is influenced greatly by the tidal effect of the ocean area as shown in Fig. 4. Therefore, there must be an optimum gate operation method to maintain the water level inside the canal. As shown in Table 2, several gate operation scenarios are evaluated and Scenario 2 was chosen as the boundary condition for this study. Fig. 5 shows the flow pattern in the West Gate and the Han River Gate of the canal for scenario 2.
2.4. Grid Size Scenarios
The trial and error method was used to determine the optimum grid system. Since there is no field measurement available for this analysis, most complicated grid cases were assumed to be the ideal one. The maximum number of grids was determined until no further changes in salt concentrations for selected locations in the channel in vertical and horizontal direction, respectively. The 3 different sites in the canal were selected for the optimum grid size analysis; 1) West Sea Gate area, 2) center of the canal way and 3) The Han River Gate area. The average salt concentrations in the upper, middle and lower layers at each station were compared when vertical layers are divided into 3 groups. Considering the above results, the grid systems to be tested are developed as shown in Table 3. The number of lateral cells was fixed to 3 cells for all cases for the sake of simplicity. The vertical grid was divided from 3 to 30 layers for 216 horizontal layers. The thickness of each layer varied from 0.2 m to 2.1 m. The horizontal grids for the channel were subdivided between 18 and 504 for 15 vertical layers in the channel. Also, the length of the horizontal direction for each cell varies from 35 m to 1000 m.
2.5. Error Analysis Method
MSE (Mean Squared Error) and MAE (Mean Absolute Error) statistics were used for error analysis can be defined as in Eq. (1) and Eq. (2), respectively.
where,
2.6. The CFL Conditions
Mathematically, the Courant–Friedrichs–Lewy condition (here after CFL condition) [25] can be described as a necessary condition for convergence while solving certain partial differential equations numerically by the method of finite differences. The CFL condition requires that the time step must be less than a certain time in many explicit time dependent computer simulations, in order to avoid incorrect results. Heuristically, this means that, if a wave is propagating across a discrete spatial grid at discrete time steps of equal length, then this length must be less than the time for the wave to travel to adjacent grid points [26]. Therefore, if the grid length decreases, the time step limit needs to be reduced accordingly. For a one-dimensional case, the CFL condition, or Courant number, C can be defined as in Eq. (3).
where,
ux = the velocity in x-direction (whose dimension is length/time)
Δt = the time step (whose dimension is time)
Δx = the length interval (whose dimension is length).
However, the CFL condition is only a necessary condition and may not be sufficient for the convergence of the finite-difference approximation of a given numerical problem. EFDC model uses explicit numerical method for horizontal calculation and implicit method for vertical calculation. Therefore, CFL method can only be good for horizontal case.
3. Results and Discussion
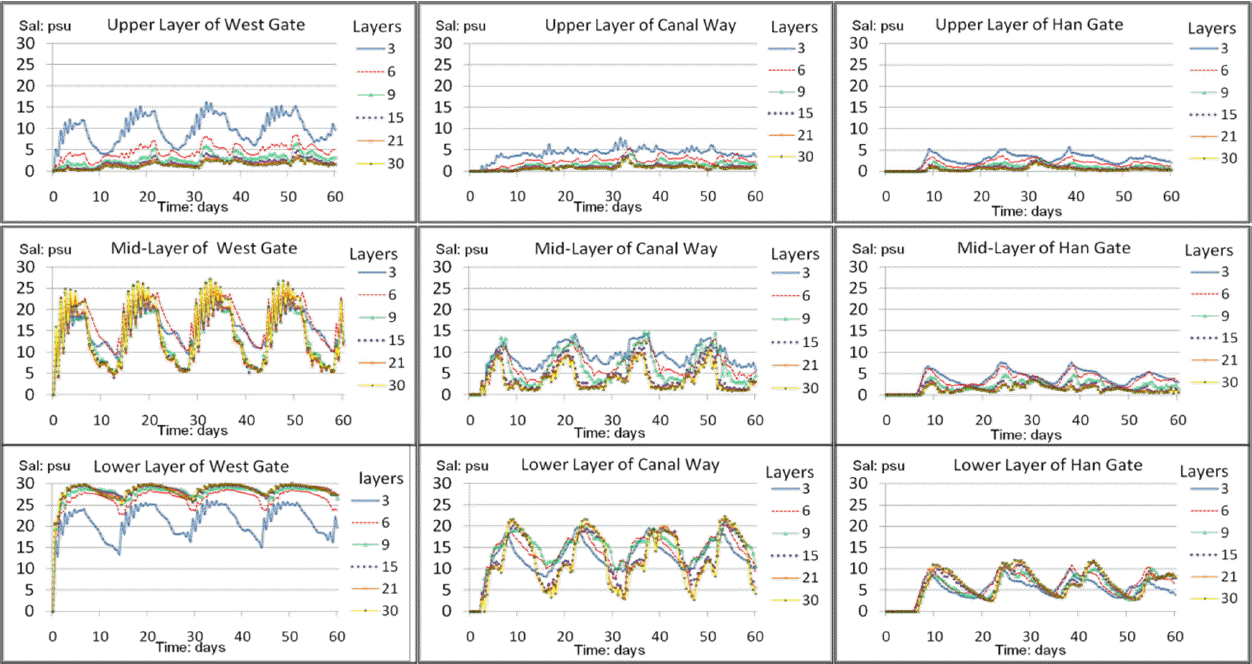
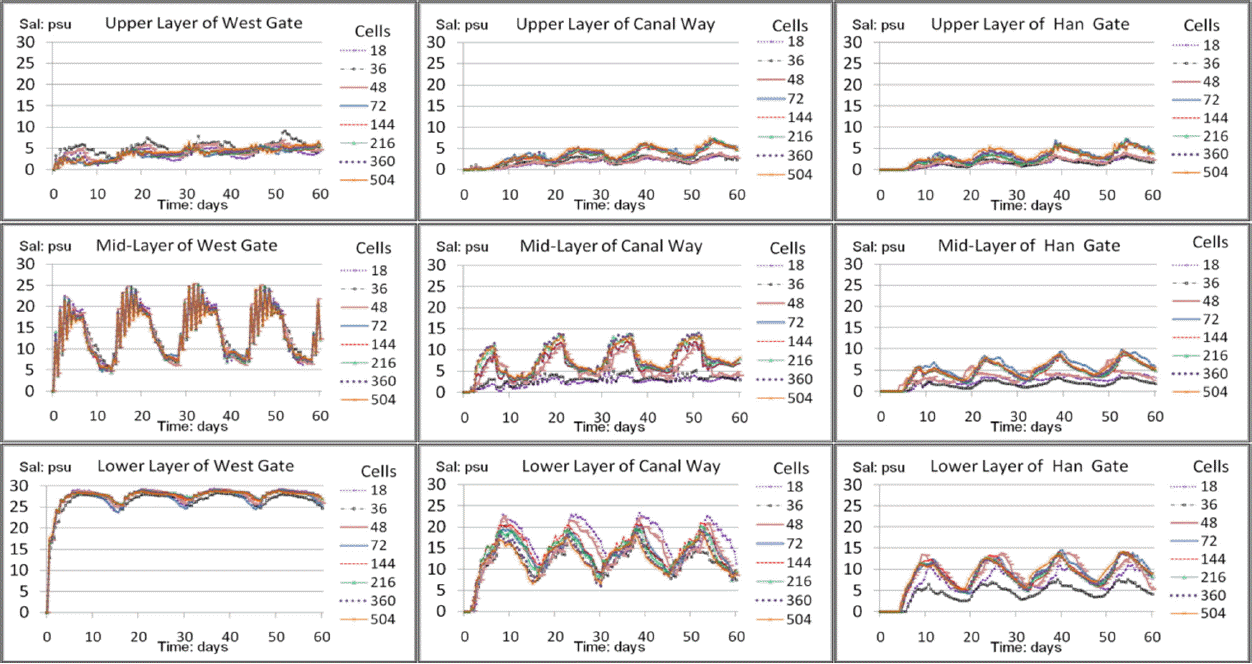
Fig. 6 and Fig. 7 show the 60 days simulation results for three selected points in the canal for different vertical and horizontal grid systems compared in this study. As shown in the figure, it seems that average salt concentrations in each layer tend to converge to a fixed value as the number of cells increases.
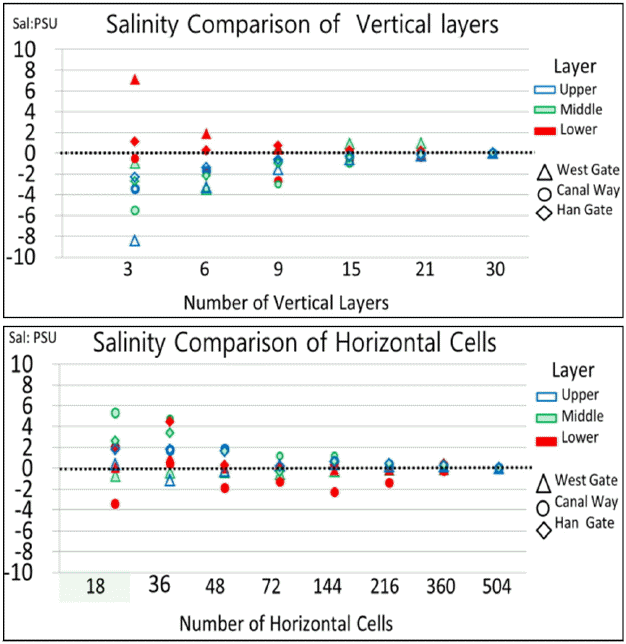
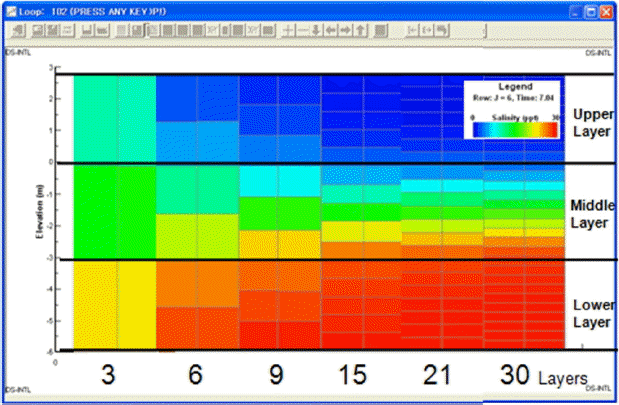
Fig. 8 shows that differences in salt concentration are negligible when 30 vertical layers and 504 horizontal divisions were used in this study, respectively. By visual inspection, it seems there must be at least 15 vertical cells and 360 horizontal cells to declare that errors seem negligible.
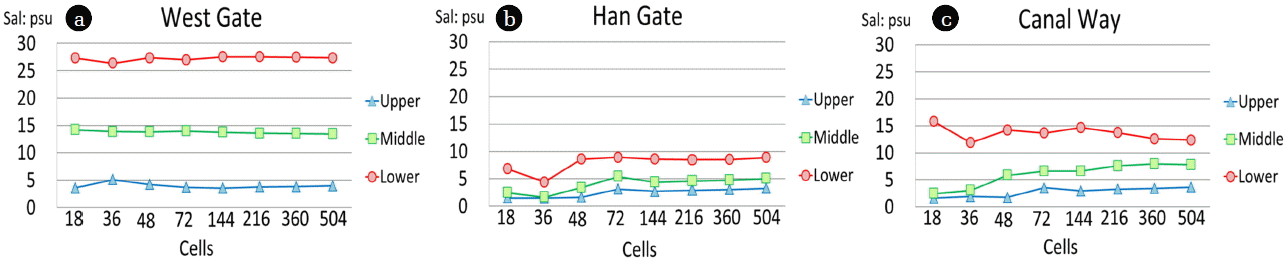
Fig. 9 shows the calculated, 60 day average vertical salt concentration at a location near the West Gate of the Ara Canal. As number of vertical layers increases, the concentration difference between the top and bottom layers increases. This indicates that the optimal number of vertical layers is essential for the accurate prediction of salinity in the study area. Fig. 10a shows changes in average salinity when vertical layers are grouped to three parts as shown in Fig. 9. As shown in this figure, the average salinity in each layer approaches to a certain point. For the bottom layer, the average salinity change seems to be stabilized when the number of vertical layers is greater than 6. However, the average concentrations in middle and upper layers decrease as the number of layers increases. This condition is caused by differences in vertical transport due to segmentation while in each cell can be regarded as completely mixed. This also indicates the importance of optimum number of grid. Fig. 10b and Fig. 10c show changes in average salinity for three vertical layers at the Canal Way and at the Han Gate locations, respectively. These figures also show similar patterns as seen in Fig. 10a.
Fig. 11a, Fig. 11b and Fig. 11c shows the average salinity concentration for different number of horizontal cells at the West Gate, in the middle of the canal way and at the Han Gate, respectively. Average concentrations in three different vertical layer groups tend to be stabilized as number of horizontal grid increases.
3.1. Error Analysis
Table 4 and Table 5 show MAE and MSE values from the most complicated grid system (30 vertical × 540 horizontal) in three different locations for different vertical and horizontal grid systems, respectively. These results show when vertical layers are 15 or more, average values of both MAE and MSE become less than 1.0. For the horizontal case, when there are more than 216 cells MAE and MSE become less than 1.0. In this simple analysis, it is suggested that 15 vertical layers and 216 horizontal cells can be regarded as optimum numbers in each direction.
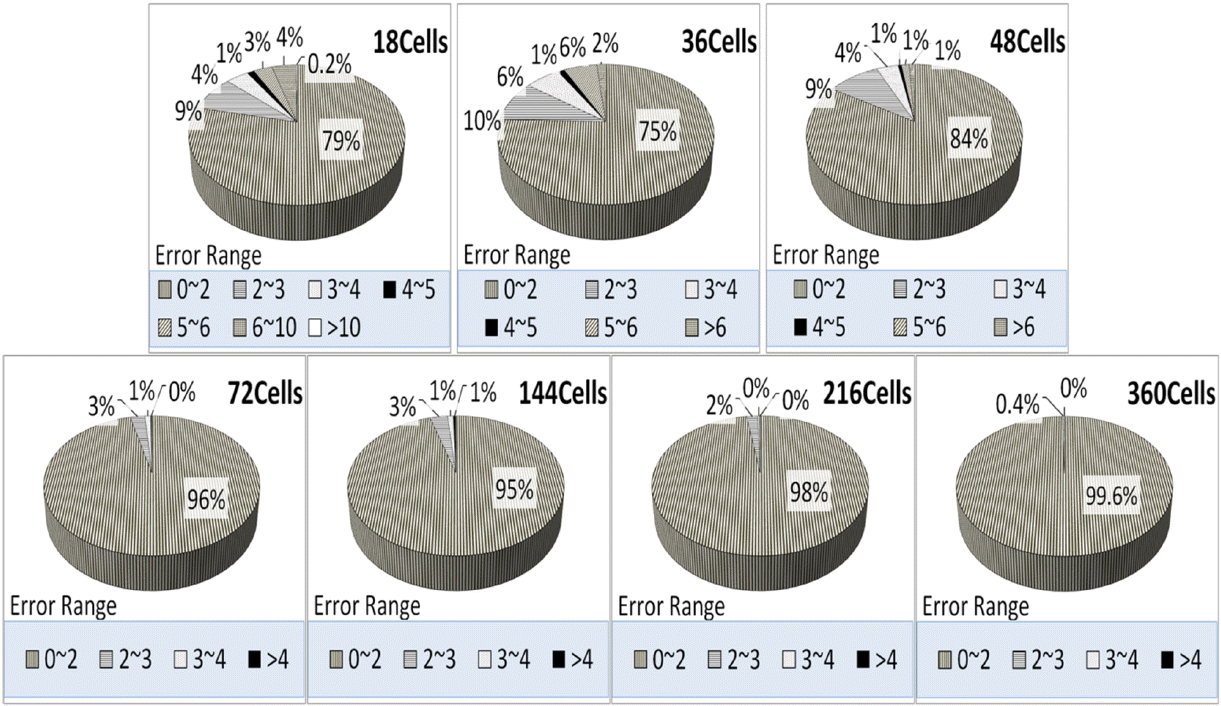
Fig. 12a and Fig. 12b show distributions of average salt concentration difference groups for different vertical layer and horizontal cells cases, respectively. These figures show that there must be at least 15 vertical layers and 72 horizontal cells to have more than 90% cases have average vertical concentration differences less than 2 ppt.
3.2. The CFL Condition Analysis
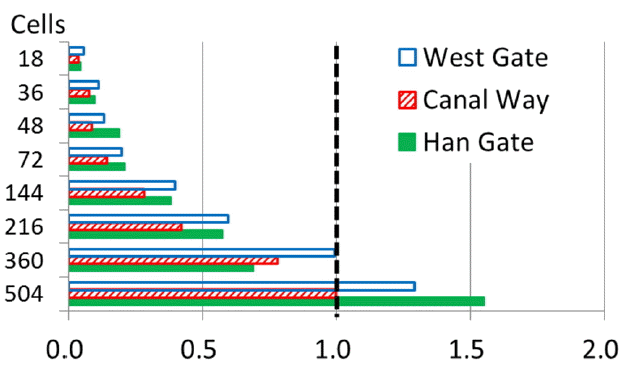
The CFL (Courant–Friedrichs–Lewy) conditions can be important in determining the optimum horizontal grid system for the study site. Though, theoretical maximum for the CFL number is 1.0, it is desirable to be less than unity. Fig. 13 shows CFL numbers estimated from three different locations in the study site. If 0.5 can be arbitrarily chosen as a limiting value for a CFL number, 144 horizontal cells can be chosen as an optimum horizontal number of cells for the study site. However, CFL number only can be applied for horizontal scale for EFDC model where explicit numerical method was used. Since EFDC model use implicit scheme for solving vertical direction, CFL number cannot be used for vertical analysis.
3.3. Determination of the Optimum Grid System for the Ara Canal
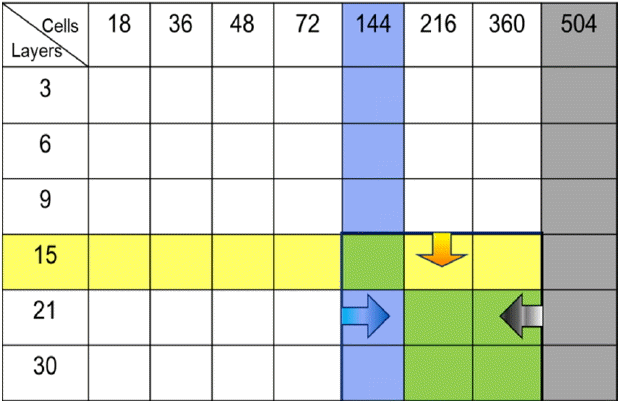
Fig. 8 shows that differences in salt concentration are negligible when 30 vertical layers and 504 horizontal divisions were used. There must be at least 15 vertical cells and 360 horizontal cells to declare that errors seem negligible. In Table 4 and Table 5, 15 vertical and 216 horizontal cells were chosen as the optimum to obtain MAE and MSE values less than 1.0. From CFL condition analysis, 144 horizontal cells were suggested as the optimum number of the horizontal grid. This study suggests that the Ara Canal has to be divided into at least 15 vertical and 144 horizontal cells to avoid significant salinity estimation error as shown in Fig. 14.
4. Conclusions
The method to determine optimum number of grid for application of the 3-D hydrodynamic model was discussed and suggested by using the Ara Canal as a test site. Salinity was chosen as a surrogate of water quality contaminant and an artificial canal was chosen as a test study site Salt concentration estimations were compared in different grid systems against the most complicated grid system. Since CFL index can only be valid for explicit numerical method, it can only be used as necessary conditions where it can be applied. MSE and MAE values seem to be appropriate to use as indices for selecting optimum grid size for the tested system. A value of 1.0 is suggested as the optimum value in the selection. This study suggests it is appropriate to subdivide at least 15 layers for 6.3 meter deep water and 144 segments in the horizontal direction for an 18 km long channel for the accurate prediction of salinity distribution of the Ara Canal, the case site, when both MSE and MAE are near to 1.0. These results will also be helpful evaluating effect of instream water quality management alternatives including aeration.