AbstractThe growth kinetics of phototrophic microorganisms can be controlled by the light irradiance, the concentration of an inorganic nutrient, or both. A multi-component kinetic model is proposed and tested in novel batch experiments that allow the kinetic parameters for each factor to be estimated independently. For the cyanobacterium Synechocystis sp. PCC6803, the estimated parameters are maximum specific growth rate (μmax) = 2.8/d, half-maximum-rate light irradiance (KL) = 11 W/m2, half-inhibition-rate light irradiance (KL,I) = 39 W/m2, and half-maximum-rate concentration for inorganic carbon (KS,Ci) = 0.5 mgC/L, half-maximum-rate concentration for inorganic nitrogen (KS,Ni) = 1.4 mgN/L, and half-maximum-rate concentration for inorganic phosphorus (KS,Pi) = 0.06 mgP/L. Compared to other phototrophs having μmax estimates, PCC6803 is a fast-growing r-strategist relying on reaction rate. Its half-maximum-rate and half-inhibition rate values identify the ranges of light irradiance and nutrient concentrations that PCC6803 needs to achieve a high specific growth rate to be a sustainable bioenergy source. To gain the advantages of its high maximum specific growth rate, PCC6803 needs to have moderate light illumination (7–62 W/m2 for μsyn ≥ 1/d) and relatively high nutrient concentrations: Ni ≥ 2.3 mgN/L, Pi ≥ 0.1 mgP/L, and Ci ≥ 1.0 mgC/L.
1. IntroductionIncreasing restrictions on carbon dioxide (CO2) discharges and depletion of petroleum reserves warrant attention to utilizing photoautotrophic microorganisms as a means to convert CO2 into biofuels and biomaterials [1–3]. A practical objective is to maximize the biomass-production rate, since the biomass embodies the sunlight energy captured by photosynthesis. Although the photosynthetic pathways in photoautotrophs are complex [4], attempting to embody all of the metabolic details is intractable for practical application to PBR design and operation. Instead, a kinetic representation that captures the core mechanisms of photoautotrophic growth is essential and efficient for design and control of PBRs.
Traditional growth kinetics of photoautotrophs has focused mainly on limitation by light irradiance (LI) [5], but such modeling is not accurate when essential nutrients (i.e., inorganic carbon (Ci), nitrogen (Ni), and phosphorus (Pi)) limit the growth rate. Even though some previous work addressed the effects of LI, Ci, Ni and Pi [6], most previous work has not attempted to identify which component (or components) is (are) rate limiting and then to quantify the kinetic response to all major limiting components.
Another unique feature of photoautotrophs is that their overall rate of photosynthesis can be inhibited by excessive LI [7]. This situation is analogous to self-inhibition kinetics for certain organic and inorganic substrates [8]. In contrast, Monod kinetics can be used to represent photosynthetic growth kinetics for individual nutrients [9].
A multiplicative kinetic model appears frequently for dual limitation by the electron donor and electron acceptor for chemotrophic microorganisms [10]. However, this multiplicative model is not directly relevant to photosynthetic microorganisms, which produce energy and reducing power from photophosphorylation and use water as an electron donor; for example, water has a fixed and essentially unlimited concentration. In addition, inorganic nutrients are anabolic building blocks essential for synthesis processes. Even when they need to be reduced (e.g., for CO2 and NO3−), they are reduced for anabolism, not respiration.
To capture these special features of phototrophic microorganisms, we propose a modified hybrid form of a multiplicative kinetic model for the specific growth rate in photosynthesis:
where μsyn is the specific growth rate, μmax is the maximum specific growth rate, KS is half-maximum-rate concentration for a given nutrient, KL is the half-maximum-rate light irradiance, KL,I is the half-inhibition-rate light irradiance, LI is the light illumination to which the microorganisms are exposed, KS,Ci, is the half-maximum-rate concentrations for inorganic carbon, KS,Ni is the half-maximum-rate concentrations for inorganic nitrogen, KS,Pi is the half-maximum-rate concentrations for inorganic phosphorus, Ci is the total concentration of the carbon, Ni is the total concentration of the nitrogen, Pi is the total concentration of the phosphorus, and square bracket with subscript ‘min’ indicates the minimum value among the individual mathematical expressions separated by commas.
The approach of Eq. (1) expresses that LI drives the oxidation of H2O to produce high-energy electrons in the form of nicotinamide adenine dinucleotide phosphate (NADPH) and adenosine- triphosphate (ATP), while synthesis of new biomass is the major sink for the electrons and ATP. The specific growth rate for synthesis is controlled by LI according to self-inhibition kinetics, the first term in Eq. (1). As long as sufficient NAD(P)H and ATP are available from photosynthesis, the synthesis growth rate is controlled solely by the most-limiting inorganic nutrient, the second term in Eq. (1), which follows single-Monod kinetics, consistent with a literature [6]. If LI and a nutrient are concurrently rate limiting, the rate of production of phototrophic-biomass is governed by the multiplicative effect of light intensity (providing the electrons and ATP) and one most-limiting nutrient (controlling synthesis, the sink for the electrons and ATP), as shown by all of Eq. (1).
In determining the specific growth rate using Eq. (1), the locally available LI inside the PBR becomes essential, since LI varies with the length of the light path and biomass concentration according to the Beer-Lambert law [11]. It is convenient to compute an average LI integrated over the entire volume of the PBR [12], as this provides a single value for LI, which we call LISA, as it is the spatially averaged value. The contents of PBRs normally are well mixed so that the photosynthetic microorganisms are exposed to LISA on average. Thus, the multiplicative form captures that LI is readily attenuated in most experimental conditions by either the system’s boundary or the biomass itself.
The primary objectives of this study are to evaluate the hybrid multiplicative model (Eq. (1) using LISA) for photoautotroph synthesis and to estimate the kinetic parameters for each of LISA, Ci, Ni, and Pi. We do so by using the cyanobacterium Synechocystis sp. PCC6803 and a specially designed series of batch experiments.
Synechocystis sp. PCC6803 is a good model photoautotroph, since it can achieve high biomass yield and is robust for wide ranges of temperature, salinity, and pH [13]. Moreover, the simple genetic structure of PCC6803 provides an opportunity to improve physiological characteristics through genetic manipulations [14]. Whether PCC6803 is wild type or genetically modified, enhancing its productivity will depend on identifying and quantifying the factors that limit its growth-rate in a photobioreactor (PBR) since ultimate goal is characterizing how to synthesize more biomass within shorter period of time.
We designed special batch experiments to allow the kinetic parameters for each factor to be estimated independently. We considered light attenuation to compute LISA inside the bioreactor and used LISA whenever LI was limiting. We evaluated the multiplicative connection between LI and the limiting nutrient, as well as self-inhibition by LISA. With estimates for all the kinetic parameters, we are able to assess the conditions that lead to a significantly high specific growth rate of PCC6803, ≥ 1/d.
2. Materials and Methods2.1. Batch-Experiment Set UpAll batch experiments were conducted in 125-mL serum bottles (Wheaton Science Products, USA) made of clear borosilicate glass and with a liquid volume of 100 mL. The experimental set up is shown schematically in Fig. S1 of Supporting Information. The mouth was sealed with a snap-on rubber stopper and an aluminum cap after filling the bottle with medium. Gas-flow controllers, connected to an air pump (KNF Neuberger, USA) with an air-filter (0.2 mm PTFE; Whatmann, USA) inlet, regulated the supply rate of CO2 by maintaining an aeration rate of 5 Lair/Lreactor/min through a tube inserted into the bottle through the rubber cap. The rapid gas bubbling make the liquid contents completely mixed, and off gas was vented out through a syringe needle while preventing mass transfer limitation of Ci.
The batch experiments were performed in a photo-incubation chamber (TC30; Conviron Inc., USA) maintained at 30°C. Light panels inside the chamber were equipped with white-fluorescent lamps and supplied photosynthetically active radiation (PAR)[15] with a controllable LI in the range of 3 – 20 W/m2 (14 – 92 mmol photons/s/m2) at the outside of the bottle. For attaining LI levels up to 48 W/m2 (221 mmol photons/s/m2), additional lamps were 92 installed. The PAR LI was measured with a PAR sensor (LI-190 Quantum sensor; LI-COR Biosciences, USA) connected to a digital multi-meter; thus, all the LI values reported in this study are on a PAR basis. The photon flux was converted to energy flux using 4.6 mmol photons/s/m2 per W/m2 [15].
2.2. Inoculum and Culture MediaPCC6803 was cultivated in a 5-L mother culture grown in a transparent 10-L reservoir bottle (KIMAX, Germany) to which we sparged filtered air (2 Lair/Lliquid/min). The bottle was continuously illuminated using fluorescent lamps (20 W/m2 on the exterior) in the same photo-incubator chamber. Non-limiting Ni, Pi, and other nutrients were supplied using standard BG-11 medium to which we added supplemental Pi using a semi-batch mode of operation (hydraulic retention time ≅ 10 d) [16]. Thus, inocula taken from the mother culture had been experiencing feast-and-famine nutrient conditions. Inoculum cultures were kept at a 730-nm optical density (OD730) of 2.3, which is defined as -log10 (I/I0), where I is the intensity of light at a 730-nm wavelength that has passed through a sample and I0 is the intensity of the light before it enters the sample.
For the batch experiments, the standard BG-11 growth medium [17] was modified to achieve limitation independently by each nutrient. For all experiments, we removed the usual amount of Na2CO3 from standard BG-11 solutions in order to have independent control of Ci; we call this BG-11C, which contained 1.5 g NaNO3, 40 mg K2HPO4·3H2O, 75 mg MgSO4·7H2O, 36 mg CaCl2·2H2O, 6 mg citric acid, 6 mg ferric ammonium citrate, 1 mg EDTA disodium salt, and 1 ml mixed trace metal solution. Each liter of trace metal solution contained 2.9 g H3BO3, 1.8 g MnCl2·4H2O, 0.22 g ZnSO4·7H2O, 0.39 g NaMoO4·2H2O, 79 mg CuSO4·5H2O, and 49 mg Co(NO3)2·6H2O in deionized water (conductivity = 18.2 MΩ ·cm) produced by Purelab Ultra (ELGA lab water, USA). Further modifications were made to BG-11C for each batch experiments, as described below, and all media were autoclaved before use.
2.3. Batch-experiment Procedures
Table 1 summarizes the four sets of batch experiments to estimate each kinetic parameter. We first used batch experiment 1 to obtain the parameters for LI-controlled kinetics first. It had ample Ni, Pi, and Ci at all times so that only LI was limiting. Using optimal-LI conditions revealed in experiment 1, we then conducted batch experiments 2, 3, and 4 to determine parameters KS,Ni, KS,Pi, and KS,Ci, respectively. The rightmost column in Table 1 indicates the range we tested for each independent variable. In all cases, the stoichiometric consumption of the limiting nutrient was small compared to its starting concentration.
Each series of batch experiment was begun by filling all the test bottles with 97 mL of modified medium according to Table 1 and adjusting the pH to 8±0.2 using a phosphate buffer (H2PO4− and HPO42− at a 7:43 mole ratio) and 0.2 M hydrochloric acid or 0.2 M sodium hydroxide. The pH was monitored using a pH meter (Accumet AB15; Fisher scientific, USA) with a glass pH electrode. We put the reactors inside the incubator overnight to establish the same temperature. The next day, we began aeration for the reactors of experiments 1 to 3 using gas-flow-rate controllers (5 Lair/Lliquid/min) and inoculated 3 mL of mother culture with disposable syringes and needles. The Ci-supply rate (mg C/Lreactor/min) was based on the CO2-aeration rate (Lair/LR/min), the CO2 content in the air (~380 ppm, v/v), the ideal-gas assumption (1 mol = 22.4 L) under standard temperature and pressure, and the molar mass of C (12 g/mol). For estimating Ci kinetics in experiment 4, we added different amounts of NaHCO3 to meet the Ci goal of each test, instead of supplying Ci by aeration; this approach allowed us to maintain a constant total-C content (= residual Ci + C in biomass) in each bottle. Although experiment 4 was not aerated, we inoculated it in the usual way and shook the bottles by hand to mix their contents at the start of the experiment and before each sampling. In addition, any produced gas was vented using a disposable syringe needle to relieve pressure build up. Since PCC6803 remained in a stable suspension for up to two days, the liquid contents for experiment 4 experienced no loss of biomass concentration due to sedimentation between samplings. The pH of BG-11C was 8±0.2, which indicates that dominant Ci species was HCO3−[18].
The initial OD730 ranged from 0.08 – 0.10, which corresponded to 21 – 27 mg/L as dry weight (DW). This low initial biomass concentration and excess concentrations of nutrients guaranteed minimal LI attenuation at the start of the experiment 1. Furthermore, we took samples during the initial 4 hours, when OD730 remained less than 0.3 (Fig. S2 in supporting information). Based on our previous research [16], the specific growth rate adjusts to the new experimental conditions for LI, Ci, Ni, and Pi within an hour; thus, the OD730 was utilized results from 1 to 4 hours.
We performed quadruplicate experiments in four reactors for each experimental condition. Thus, we present the average specific growth rate with a standard deviation from the 4 reactors. Variability was small among the tests and may have originated from small differences in acclimation to the new conditions, inoculum size, carryover of nutrients with the inoculums, and sampling timing.
2.4. Control ExperimentsWe also carried out an upper control experiment with all nutrients present and a series of lower control experiments with one nutrient totally absent (Fig. S2 of the Supporting Information). The upper control results indicate that the maximum μ was > 1.6/d. For the lower controls, the inocula were washed three times in 0.9% NaCl solution to remove residual nutrient from the inoculum’s growth medium before conducting each experiment. The lower control results document that eliminating any one nutrient suppressed biomass growth so that the biomass increase over 4 h was a maximum of 8.0 mg/L or 0.03 OD730. Because the change in biomass was so small in the lower controls, we were able to use directly the biomass concentrations in non-control experiments (Table 1).
2.5. Sampling and Analytical MethodsThe growth kinetics of PCC6803 were monitored by analyzing 2-mL liquid samples taken at 0, 1, and 4 hours with a disposable syringe using a needle inserted through the rubber cap. OD730 was directly measured with a UV-visible spectrophotometer (Cary 50 Bio; Varian Inc., USA) at a wavelength of 730 nm and was converted to DW using calibration curve that we determined for PCC6803, shown in Fig. S3 of Supporting Information. For the calibration, DW was determined using total suspended solids (Method 2540D in Standard Methods) [19].
The specific growth rate was computed for synthesis based on biomass concentrations in samples taken at the beginning and end of a time interval:
where μ is the observed net specific growth rate (/d), μsyn is the synthesis specific growth rate (/d), b is the endogenous decay rate (/d), and X1 and X4 are the biomass concentrations (expressed by mg DW/L) at time 1 and 4 hours (t1 and t4), respectively. Independently, b was estimated by the decrease of biomass concentration under complete darkness for one day; the value was 0.056/d, as presented in Table S1 of Supporting Information.
To obtain the best estimates of the kinetic parameters for LI, Ni, Pi and Ci from each set of experiments, we conducted non-linear regression using computer software (Sigmaplot10; Systat Software Inc., USA) that related the observed μsyn = m + b to the spatially averaged light intensity (LISA) and the concentration of the limiting nutrient at a fixed LISA. For estimating parameters associated with Ni, Pi, and Ci kinetics in experiments 2 – 4, we employed the best-fit constants for LI revealed previously in experiment 1. This strategy made it possible for us to use the experimental data for each nutrient to estimate only one corresponding parameter (KS).
2.6. Light AttenuationAverage LI integrated over the entire PBR volume representing spatially averaged value, LISA, was computed in W/m2 as PAR based on these assumptions: a transparent cylindrical shape, uniform illumination from all sides, no light absorption by the biomass-free medium, no top and bottom effects, and light attenuation according to the Beer-Lambert law [12]. Supporting Information (Fig. S4) provides details of the geometry involved in the calculation. The equation for LISA is:
where LI0 = LI at the light-entry surface (W/m2), ɛ = the Beer-Lambert constant (m3/g/m), X = biomass concentration (g/m3), and d = depth of light path from the light-entry surface (m). Suh and Lee[11] verified that e for Synechococcus sp. PCC6301 is 0.255 m3/g/m. Our preliminary study with PCC6803 found a similar value from light-attenuation experiments conducted within our ranges of biomass concentration using PCC6803. Therefore, we utilized ɛ= 0.255 m3/g/m to calculate LISA, and the LISA was used in Eq. (1).
3. Results and Discussion3.1. Substrate-Inhibition Kinetics for LISATable S2 shows the calculated LISA values using the measured biomass concentrations and LI0 at the start of each batch experiment. With LI0 outside the batch reactor varying from 2.6 to 48 W/m2, LISA ranged from 2.3 to 43 W/m2. The attenuation was ~13% of LI0 with the biomass concentrations of ~ 27 mg DW/L.
Fig. 1 shows the observed μsyn values based on biomass measurements taken at 1 and 4 hours for each LISA. These results demonstrate the expected trends for LI self-inhibition kinetics: increasing μsyn for LISA up to about 8 W/m2, relatively steady μsyn from about 10 to 25 W/m2, and decreasing μsyn for LISA greater than ~30 W/m2. The highest observed μsyn was approximately 1.5/d for LISA of ~30 W/m2.
Non-linear regression yielded μmax of 2.8/d, KL = 11 W/m2, and KL,I = 39 W/m2. The value of μmax was significantly larger than 1.5/d because of LI inhibition, which is quantified by the relatively low value of KL,I. Based on the LI kinetic model, PCC6803 achieve a benchmark μsyn ≥ 1/d when LISA is in the range of 7 to 62 W/m2.
3.2. Monod Kinetics for Ni, Pi, and CiUsing the results for LI kinetics (experiment 1, which had sufficient Ni, Pi, and Ci), we could obtain parameter estimates for the growth kinetics of PCC6803 for each nutrient limitation (experiments 2 – 4). We chose LI0 = 18 W/m2 to keep the initial LISA at around 16 W/m2, which is in the range where LISA does not have a sensitive effect on μsyn (Fig. 1). In each experimental series, we computed the LI-adjusted μmax value from Eq. (1) and the actual LISA value; we call this value μsyn, LI.
Experiment 2 evaluated the kinetics for Ni limitation, and Fig. 2 shows μsyn for Ni varying from 0 to 124 mgN/L. The results clearly exhibit a Monod-type saturation pattern with μsyn saturating at μsyn,LI = 1.6/d (based on LI limitation from experiment 1). Non-linear regression (R2 = 0.97) yields KS,Ni = 1.4 mgN/L. This value means that the NO3− concentration in a PBR should be greater than 13 mgN/L to maintain 90% of the maximum specific growth rate, but the rate is slowed to 10% of the maximum value when the NO3− concentration falls below 0.16 mgN/L. Serious Ni-limitation of cyanobacteria is highly undesirable, because it can cause visible chlorosis, or yellowish coloring of the cells due to the degradation of thylakoid membranes [20] or a decrease in their chlorophyll content [21]. Keeping Ni over 2.3 mgN/L in a PBR is necessary for growing PCC6803 at a benchmark μsyn of at least 1/d (with LISA~16 W/m2).
Fig. 3 shows the photosynthetic specific growth rate as a function of the total-Pi concentration in experiment 3. With the pH held constant at 8±0.2, the dominant Pi species were H2PO4− and HPO42−, present at a molar ratio of 7:43. Thus, the corresponding ranges for H2PO4− and HPO42− concentrations were 0.14–3.8 mgP/L and 0.86–23 mgP/L, respectively. The experiments showed an almost constant μsyn value (1.6/d) for total-Pi concentrations of 3 mgP/L and higher. Only when the total-Pi concentration was less than 1 mgP/L, the lowest concentration tested except the control, did μsyn show a slightly lower value, 1.4/d.
Applying μsyn,LI (1.6/d) gave a good match of the Monod function to the experimental results and led to an estimated KS,Pi of 0.06 mgP/L for total Pi (R2 = 0.99). This low KS,Pi value indicates very high affinity for Pi and that it is not necessary to maintain a high concentration of Pi in the PBR, compared to what is required for Ni. For example, maintaining μsyn ≥ 1/d demands that the total-Pi concentration be at least 0.1 mgP/L.
Although a high specific growth rate does not require a high Pi concentration, it is very important to monitor the Pi concentration and ensure that it does not become seriously limiting. Previous studies reported that a deficiency of Pi may have an important impact on photosynthetic activity, since P is a key component in energy transfer and signal transduction, as well as lipid biosynthesis for algae and cyanobacteria [22]. Once Pi-limitation sets in, it may cause severe change of photosynthesis in PCC6803, as has been noticed for other cyanobacteria [23]. Problems of Pi depletion can be exacerbated when complexation of HPO42− and PO43− with cations such as Ca2+ and Mg2+ reduces the availability of Pi by forming octacalcium phosphate (Ca8(HPO4)2(PO4)4·5H2O) and hydroxyapatite (Ca10(OH)2(PO4)6), particularly as the pH increases [24].
In experiment 4, we varied the Ci concentration using NaHCO3 as the Ci source, not by aeration. This ensured that our results were not confounded by mass transfer resistance from CO2(g) to CO2(aq). The pH was maintained at 8 with a phosphate buffer; thus, the mass distribution between CO2(aq) and HCO3−, the Ci sources for PCC6803 [25], was fixed at a molar ratio of 1:49. The corresponding test ranges for CO2(aq) and HCO3- were 0–5.6 mgC/L and 0–279 mgC/L, respectively.
Fig. 4 illustrates a clear Monod-like relationship between μsyn and the Ci concentration. The experimentally observed value peaked at around 1.5/d for Ci. Setting the maximum specific growth rate as μsyn,LI = 1.6/d (from LISA and experiment 1) gave an excellent match with the experimental results, and nonlinear regression estimated KS, Ci = 0.6 mgC/L for total Ci. Thus, PCC6803 had a high affinity for Ci when HCO3− was the dominant species at pH around 8. Due to its large dominance over CO2(aq) in solution, HCO3− probably was the species taken up by PCC6803 in these experiments [26], and KS,Ci, = 0.6 mgC/L probably corresponds to the KS value for HCO3−. The Ci concentration needed to achieve μsyn of 1/d is approximately 1.0 mgC/L, which is intermediate between 0.1 mgP/L and 2.3 mgN/L.
3.3. Interpretation of Kinetic Parameters for the Nutrients
Table 2 compares our LI parameters to literature values obtained for other cyanobacteria and algae. Our KL value was similar to other results (6 – 18 W/m2), but KL,I was considerably smaller than previously reported values. Most notably, Synechococcus sp. PCC7942 had a reported KL,I of 97 W/m2 [27], although light attenuation was not considered in the estimation. Using LISA instead of LI0 would make their KL,I smaller: ~77 W/m2 based on the analysis presented in Supporting Information (Table S3 and Fig. S5). Thus, the comparison of KL,I values suggests that PCC6803 is relatively more sensitive to photo-inhibition than are other phototrophs that have been evaluated. However, significant negative impacts of LI self-inhibition require a substantially greater LISA value than ~62 W/m2 (Fig. 1).
Table 3 also shows all of our KS and μmax values together with literature values obtained with other algae or cyanobacteria. Compared to ranges for algal species with reported μmax values (0.7 – 1.7/d), PCC6803 had by far the highest μmax (2.8/d), although the highest observed μsyn,LI was 1.6/d due to photo-inhibition. The relatively high μmax values suggests that PCC6803 behaves as an r-strategist, or a copiotroph that employs a rapid-growth strategy [28] that gives it a competitive advantage when conditions allow it to avoid significant limitation by LI or any of the inorganic nutrients.
The values of KS,Ci, reported for algae (0.002–0.005 mgC/L) are significantly lower than for PCC6803. This means that the growth rate of PCC6803 can be more easily limited by Ci, compared to algae, when an imbalance between supply and utilization of CO2 occurs. Thus, PCC6803 needs to have a sufficient Ci supply rate to avoid HCO3− limitation, which would counteract it growth-rate advantage over algae.
Due to PCC6803’s relative sensitivity to the Ci concentration, it would be possible that high pH may slow the Ci-uptake kinetics by changing the dominant Ci form to CO32−, with CO2(aq) becoming negligible because the concentrations of available Ci species - CO2(aq) and HCO3− - are determined by the pH [25]. The pH also affects the complexation equilibria of cationic and anionic species that can precipitate with Ci. High pH by active photosynthesis can lower the available Ci by precipitating it as part of CaCO3.
Similar to Ci, PCC6803 is more easily limited by low Ni, compared to other phototrophs for which we have reports [16, 29]. Although our estimated KS,Ni (1.4 mgN/d) is not far from a literature value (5.3 mgN/L) obtained for Spirulina platensis [9], which, like Synechocystis, is a non-diazotrophic cyanobacterium [20], several algae show KS,Ni values about one order of magnitude lower (0.02~0.16 mgN/L).
Unlike for Ci and Ni, PCC6803 is not more severely limited by Pi than are other phototrophs. A study using the cyanobacterium Synechococcus sp. PCC7942 reported KS,Pi = 0.07 mgP/L [30], almost identical with our result (0.06 mgP/L). In addition, the KS,Pi values of several algae were in a similar range, 0.02 to 0.12 mgP/L, although one report was much higher [31]. Such similarity may indicate that utilization mechanisms of Pi are invariant.
4. ConclusionsWe use a series of special batch experiments to estimate parameter values for a multi-component kinetic model of photoautotrophic growth. Results for the cyanobacterium Synechocystis PCC6803 quantify its growth-rate limitation by LISA or the concentration of Ci, Ni, or Pi. With μmax = 2.8/d, PCC6803 is an r-strategist (or copiotroph) that can grow fast when light and nutrients do not limit. This is ideal when the goal is to maximize the biomass production rate, such as for biomass production as a renewable source of biofuels and biomaterials. To gain the advantages of its high maximum specific growth rate, PCC6803 needs to have moderate light illumination (7 – 62 W/m2 for μsyn ≥ 1/d) and relatively high nutrient concentrations: Ni ≥ 2.3 mgN/L, Pi ≥ 0.1 mgP/L, and Ci ≥ 1.0 mgC/L.
AcknowledgementsWe are grateful to the Advanced Research Projects Agency-Energy (ARPA-E) of the United States Department of Energy for their generous financial support. We thank Drs. Willem Vermass, Roy Curtiss, Rosa Krajmalnik-Brown, and David Nielsen and their laboratories in, respectively, the School of Life Sciences, School of Sustainable Engineering and the Built Environment, and the School for Engineering of Matter, Transport and Energy at Arizona State University for assistance and advice on PCC6803, experimental designs, and data analysis. In addition, This work was financially supported by the Research Program for Agriculture Science & Technology Development (Project No. PJ01082403 2015), Rural Development Administration, Korea.
NotesSupplementary Information Supplementary data to this article can be found online at http://eeer.org. References1. Wahlen BD, Morgan MR, McCurdy AT, et al. Biodiesel from Microalgae, Yeast, and Bacteria: Engine Performance and Exhaust Emissions. Energy & Fuels. 2012;27:220–228.
2. Campbell JE, Lobell DB, Field CB. Greater Transportation Energy and GHG Offsets from Bioelectricity Than Ethanol. Science. 2009;324:1055–1057.
3. Rittmann BE. Opportunities for renewable bioenergy using microorganisms. Biotechnol Bioeng. 2008;100:203–212.
4. Berg JM, Tymoczko JL, Stryer L. Biochemistry. 6 edW.H. Freeman; 2006.
5. Fernandez FGA, Camacho FG, Perez JAS, Sevilla JMF, Grima EM. A model for light distribution and average solar irradiance inside outdoor tubular photobioreactors for the microalgal mass culture. Biotechnol Bioeng. 1997;55:701–714.
6. Wolf G, Picioreanu C, van Loosdrecht MCM. Kinetic modeling of phototrophic biofilms: The PHOBIA model. Biotechnol Bioeng. 2007;97:1064–1079.
7. Ogbonna JC, Tanaka H. Light requirement and photosynthetic cell cultivation - Development of processes for efficient light utilization in photobioreactors. J Appl Phycol. 2000;12:207–218.
8. Andrews JF. A mathematical model for continuous culture of microorganisms utilizing inhibitory substrates. Biotechnol Bioeng. 1968;10:707–723.
9. Cornet JF, Dussap CG, Cluzel P, Dubertret G. A structured model for simulation of cultures of the cyanobacterium Spirulina-Platensis in photobioreactors: II. Identification of kinetic-parameters under light and mineral limitations. Biotechnol Bioeng. 1992;40:826–834.
10. Bae W, Rittmann BE. Responses of intracellular cofactors to single and dual substrate limitations. Biotechnol Bioeng. 1996;49:690–699.
11. Suh IS, Lee SB. A light distribution model for an internally radiating photobioreactor. Biotechnol Bioeng. 2003;82:180–189.
12. Evers EG. A model for light-limited continuous cultures- Growth, shading, and maintenance. Biotechnol Bioeng. 1991;38:254–259.
13. Mikami K, Kanesaki Y, Suzuki I, Murata N. The histidine kinase Hik33 perceives osmotic stress and cold stress in Synechocystis sp PCC 6803. Mol Microbiol. 2002;46:905–915.
14. Angermayr SA, Hellingwerf KJ, Lindblad P, de Mattos MJT. Energy biotechnology with cyanobacteria. Curr Opin Biotechnol. 2009;20:257–263.
15. McCree KJ. Test of current difinitions of photosynthetically active radiation against leaf photosynthesis data. Agric Meteorol. 1972;10:443–453.
16. Kim HW, Vannela R, Zhou C, Harto C, Rittmann BE. Photoautotrophic Nutrient Utilization and Limitation During Semi-Continuous Growth of Synechocystis sp PCC6803. Biotechnol Bioeng. 2010;106:553–563.
17. Rippka R, Deruelles J, Waterbury JB, Herdman M, Stanier RY. Generic assignments, strain histories and properties of pure cultures of cyanobacteria. J Gen Microbiol. 1979;111:1–61.
18. Snoeyink VL, Jenkins D. Water Chemistry. New York: John Wiley & Sons; 1980.
19. Eaton AD, Clesceri LS, Rice EW, Greenberg AE, Franson MAH. Standard Methods for the Examination of Water and Wastewater. 21 edWashington, D.C: American Public Health Association; 2005.
21. Stevens SE, Balkwill DL, Paone DAM. The effects of nitrogen limitation on the ultrastructure of the cyanobacterium Agmenellum-Quadruplicatum. Arch Microbiol. 1981;130:204–212.
22. Guschina IA, Dobson G, Harwood JL. Lipid metabolism in cultured lichen photobionts with different phosphorus status. Phytochemistry. 2003;64:209–217.
23. Stevens SE, Paone DAM, Balkwill DL. Accumulations of cyanophycin granues as a result of phosphate limitation in Agmenellum-Quadruplicatum. Plant Physiol. 1981;67:716–719.
24. Lu X, Leng Y. Theoretical analysis of calcium phosphate precipitation in simulated body fluid. Biomaterials. 2005;26:1097–1108.
25. Ogawa T, Kaplan A. Inorganic carbon acquisition systems in cyanobacteria. Photosyn Res. 2003;77:105–115.
26. Shibata M, Ohkawa H, Katoh H, Shimoyama M, Ogawa T. Two CO2 uptake systems in cyanobacteria: four systems for inorganic carbon acquisition in Synechocystis sp strain PCC6803. Funct Plant Biol. 2002;29:123–129.
27. Wang JS, Araki T, Ogawa T, Matsuoka M, Fukuda H. A method of graphically analyzing substrate-inhibition kinetics. Biotechnol Bioeng. 1999;62:402–411.
28. Rittmann BE, McCarty PL. Environmental Biotechnology: Principles and Applications. McGraw-Hill Publishing Co; 2001.
29. Kim HW, Vannela R, Zhou C, Rittmann BE. Nutrient Acquisition and Limitation for the Photoautotrophic Growth of Synechocystis sp PCC6803 as a Renewable Biomass Source. Biotechnol Bioeng. 2011;108:277–285.
30. Ritchie RJ, Trautman DA, Larkum AWD. Phosphate uptake in the cyanobacterium Synechococcus R-2 PCC 7942. Plant Cell Physiol. 1997;38:1232–1241.
31. Aslan S, Kapdan IK. Batch kinetics of nitrogen and phosphorus removal from synthetic wastewater by algae. Ecol Eng. 2006;28:64–70.
32. Lee HY, Erickson LE, Yang SS. Kinetics and bioenergetics of ligh-limited photoautotrophic growth of Spirulina-Platensis. Biotechnol Bioeng. 1987;29:832–843.
33. Lee DY, Rhee GY. Kinetics of growth and death in Anabaena flos-aquae (cyanobacteria) under light limitation and supersaturation. J Phycol. 1999;35:700–709.
34. Fouchard S, Pruvost J, Degrenne B, Titica M, Legrand J. Kinetic Modeling of Light Limitation and Sulfur Deprivation Effects in the Induction of Hydrogen Production With Chlamydomonas reinhardtii: Part I. Model Development and Parameter Identification. Biotechnol Bioeng. 2009;102:232–245.
35. Yun YS, Park JM. Kinetic modeling of the light-dependent photosynthetic activity of the green microalga Chlorella vulgaris. Biotechnol Bioeng. 2003;83:303–311.
36. Novak JT, Brune DE. Inorganic carbon limited growth-kinetics of some fresh-water algae. Water Res. 1985;19:215–225.
37. Gotham IJ, Rhee GY. Comparative kinetic-studies of nitrate-limited growth and nitrate uptake in photoplankton in continuous culture. J Phycol. 1981;17:309–314.
Fig. 1Specific growth rates (μsyn) for the range of LISA values for experiment 1 and the corresponding regression results using the self-inhibition kinetic model (inset). 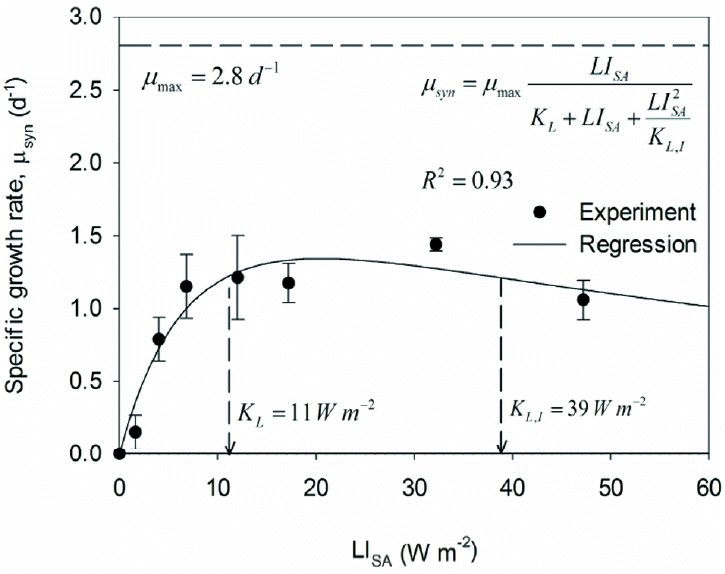
Fig. 2Specific growth rates (μsyn) for the range of Ni concentrations for experiment 2 and the corresponding regression results using the Monod model (inset). 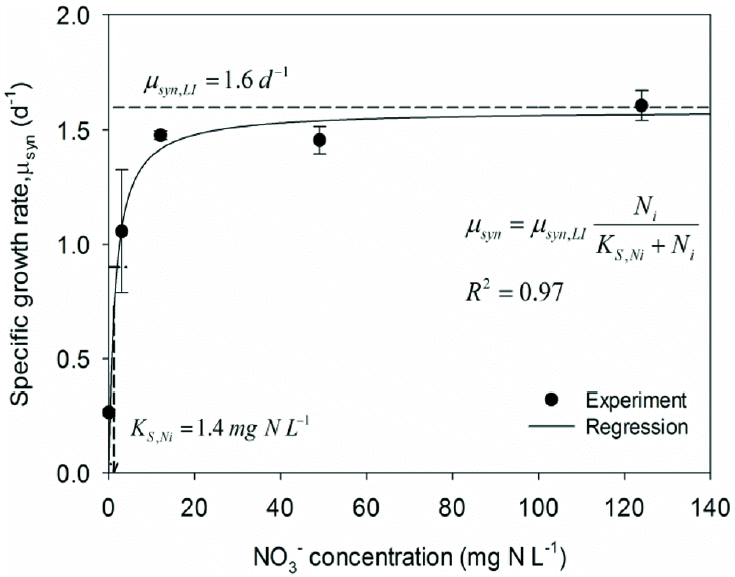
Fig. 3Specific growth rates (μsyn) for the range of Pi concentrations for experiment 3 and the corresponding regression results using a Monod model (inset). At pH 8, the molar ratio of H2PO4− : HPO42− = 7:43, while H3PO4 and PO43− are negligible. 
Fig. 4Specific growth rates (μsyn) for the range of Ci concentrations for experiment 4 and the corresponding regression results using a Monod model (inset). At pH 8, the molar ratio of CO2(aq) : HCO3− : CO32− =1.9 : 97.6 : 0.5. 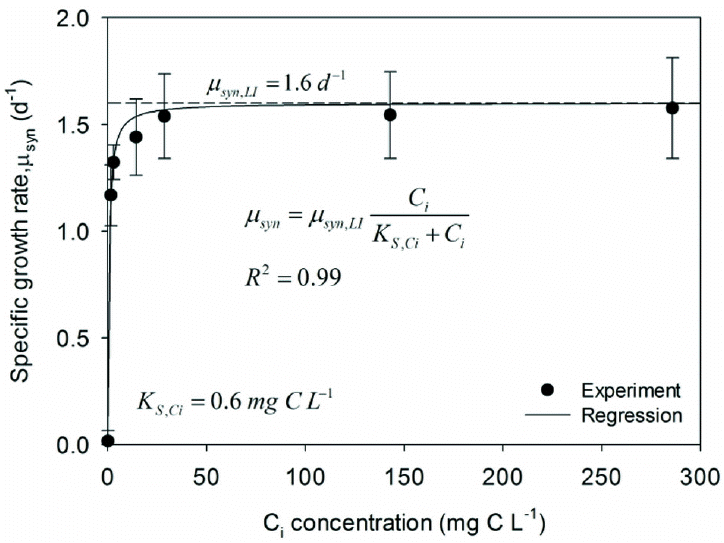
Table 1Experimental Design for the Estimation of Kinetic Constants (The experimental set up for these experiments is shown schematically in Fig. S1 in Supporting Information.)
Part per million by volume from NOAA/ESRL (http://www.esrl.noaa.gov/gmd/ccgg/trends/). Table 2Comparisons of Kinetic Parameters using the Self-inhibition Model for Light Irradiance for Cyanobacteria and Algae
Table 3Comparisons of μmax and KS Values for Ci, Ni, and Pi using Monod Kinetics with a Range of Phototrophic Microorganisms
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||