AbstractResearch into gas flow motion as a transported phase and pollutant – particulate matter (PM) is of crucial importance, their changes in particular areas of the object require knowledge of improving the apparatus. A cyclone is considered one of the most popular devices due to the new modified multi-channel design that involves combined separation and filtration phenomena. The findings of an accurate numerical model provide an opportunity to verify long-term experimental studies. In addition, it is possible to determine the impact of the designed principal elements of the structure comprising secondary gas inlets, inner slits and the convex bottom on gas and PM motion through verification conducting experimental research. The study focuses on simulating the upgraded cyclone using the SST k-omega model. The research has been conducted under the specified gas flow conditions such as high temperature and relative humidity (aggressive) gas and presents the results of the physical model to compare with. To achieve greater computational accuracy, a digital model of the cyclone made of specific volumetric elements has been developed thus expanding the grid and stepping to form the boundary zone. As a result, numerical simulation results differ by no more than 12.8% compared to the experimental studies results.
1. IntroductionCyclones are widely used gas treatment equipment for removing particulate matter from gas flow [1]. Cyclones operate under the action of centrifugal forces, and therefore are broadly applied in industry as the first-stage equipment for removing particulate matter from industrial gas. Conventional and multi-channel cyclones are available. The first type of cyclones falls into two categories such as those of reverse and axial flow and are subject to the direction of gas flow in the inlet and outlet. Compared to reverse flow cyclones, the structure of axial flow cyclones is more suitable for gas-liquid separation with less turbulence and pressure drop, is of smaller dimensions and easy applied to parallel multi-cyclone assembly. However, the treatment process involves centrifugal forces in both types of conventional cyclones.
Multi-channel cyclones are classified as innovative technology besides the effect of centrifugal forces observed in which, the additional removal of particulates takes place in the channels. Higher effectiveness of removing particulate matter from the above introduced equipment is achieved by combining two treatment principles in a single device. The principles involve centrifugal removal and multiple filtrations through a layer of dust formed in the gaps between the curvilinear elements of the channels of the cyclone.
The simple structure, low cost and noise and application under high temperatures and pressure have made cyclones commonly used in oil refineries, chemical industry and many other fields.
However, despite the relatively widespread use of cyclones, no research has been conducted yet to accurately and comprehensively assess the trapped particulate matter. Considering all structural features and processes taking place in the devise, the theoretical calculation method should allow assessing effectiveness. Several methods have been currently used for assessing the treatment effectiveness of cyclones. The method of calculating cyclones [2] is one of the developed techniques based on empirical probability functions describing parameters for the effective fractional collection of particulates in the cyclone and the dispersive composition of particulate matter. Nevertheless, the introduced method is not accurate enough.
The effectiveness of the operating cyclone is best characterized by the degree of removing particulates and pressure drop between inlet and outlet openings. The parameters may vary depending on flow rate at the inlet. Pressure drop increases continuously along with a rise in flow rate [3, 4]. However, first, an increase in flow rate results in the elevated effectiveness of removing particulates and then begins decreasing [4]. To assess removal effectiveness, a critical flow rate at the inlet is frequently emphasized as the maximum flow rate at the inlet (VMEIV).
The carried out research has also shown that, along with cyclone applications, the flow characteristics of fluid and particulate matter as well as cyclone applications are highly sensitive to geometrical parameters and operating conditions. Recent research explains that gas flow and particulate matter under effect are strongly influenced by vortex flow and the resulting structural elements such as vortex finder parameters, the length of flow guides and the inclination angle [5, 6], the length of cylindrical and conical segments [7], inlet dimensions [8–10] and the diameter of the cyclone of the main casing (separation chamber) [1, 11]. The diameter of the conical section [12] and the depth of the vortex finder are geometrical elements having a less important effect on the operation of the cyclone.
To avoid vortex flow in the multi-channel cyclone, a steady gas flow at the same rate is maintained. Therefore, the diameter of channels is uniformly reduced thus compensating for the loss of path pressure and maintaining an equal rate in the channels. Studies have demonstrated that the symmetrical arrangement of inner elements allows avoiding reverse flows between adjacent channels. This results in lower flow turbulence and more effective deposition of particulate matter.
As reported by one of the studies [11], a rise in the size of the cyclone reduces pressure drop by 35% thus increasing effectiveness. However, some cases indicate that the size of the cyclone is reduced due to limited space and in order to optimize the performance of the cyclone. Although the overall height of the cyclone and the diameter of the separation chamber are considered fixed, the length of the cylindrical section may vary conforming to the length of the conical part. A similar study was conducted by Elsayed and Lacor [12] when simulation was used for reducing pressure drop in the cyclone. The study demonstrated that the diameter and inlet height and width of the vortex finder and the total height of the cyclone were found to be the most significant geometrical parameters.
Different simulation programmes are employed for analysing the operation of cyclones and for simulating gas flows containing particulate matter of different diameters. The Reynolds stress turbulence (RST) model provides an accurate prediction of creating flow properties, axial rate, tangential rate and pressure drop in the cyclone [13, 14]. The k–ɛ turbulence model is based on the viscosity concept of isotropic vortexes for Reynolds stress expressions. In the case of complex flows with gravitational forces or stress fields, this assumption seems to be oversimplified.
Muschelknautz, and Trefz [15] attempts to take into account the singularities of the flow adjustment device, the friction of the walls, multi-fractionality and the concentration of particulate matter entering collection devises of the cyclone. The paper [16] proposes a statistical correlation of assessing fractional effectiveness satisfactorily compatible with experimental data on the cyclones of different geometry.
A few factors, including the geometry of the cyclone, the properties of gas flow in the cyclone and the features of particulate matter, have an effect on simulating cyclone operation. Therefore, a detailed examination and description of the operating cyclone having an appropriate structure opting for relevant models consistent with experimental results is a crucial issue, which is expected to be a useful tool for improving the structural elements of the cyclone and achieving higher effectiveness of the cyclone. The new type cyclone has inner elements which change the gas flow dynamic as opposed to the gas flow processes in conventional cyclone. This article was dedicated to the comparison of two similar basis methods k-epsilon and k-ω (omega), their similarities and difference.
2. Numerical Simulation Methodology for Particulate Matter and Gas Flow ProcessesNumerical simulation is performed to determine dynamic parameters for gas flow polluted with fine-dispersed particulate matter, to explore the effect of an aggressive gas flow on the operation of the advanced multi-channel cyclone and to define optimal parameters thus avoiding additional costs for the production, adjustment and improvement of an experimental bench.
At the first stage, the experimental bench of the advanced multi-channel cyclone was developed, and experimental studies were performed. Numerical object geometry was created using a CAD vector graphic editor, employing parametric object design, creating planar and spatial elements. Parameters for the numerical multi-channel cyclone were selected in line to those for the experimental bench of the advanced multi-channel cyclone. The research and analysis of the numerical model for the two-phase (gas (air), particulate matter) flow in the cyclone were performed applying the Fluent subprogram of the ANSYS software package.
Studies done by other researchers have frequently been limited to a single viscosity model often employed in the standard option or by setting parameters automatically. For that purpose, different viscosity models were selected, and model modifications were applied for sensitivity analysis.
Calculations involved models k-epsilon and k–ω (omega) for turbulent viscosity and their modifications – k–ɛ (epsilon) and k–ɛ RNG (Re–Normalisation Group) (advanced model for turbulent kinetic energy (TKE) and kinetic energy dissipation rate) and k–ω SST (TKE and a comparative rate of kinetic energy dissipation) [17]. The application of the k–ɛ model assists in solving a system of two nonlinear diffusion equations – TKE density (kρ) and kinetic energy dissipation rate (ɛ) – the rate at which TKE converts to heat due to viscous friction. Standard k–ɛ (Eq. (1) and (2)) and k–ɛ RNG (Eq. (3) and (4)) models are expressed in the form of partial derivatives [18]:
where k – turbulent kinetic energy, m2/s2; Gk – TKE variations under the effect of the average rate gradient equal to Gk = μtS2 applying the Businescu hypothesis; μt – turbulent dynamic viscosity; S – strain tensor; Gb – TKE variations under the effect of buoyancy equal to
; β – the coefficient of temperature expansion; Prt – the turbulent Prandtl number for energy; gi – gravity vector taking direction i; YM – fluid rate distribution under the effect of a displacement in space at turbulent compression equal to
; Mt – the coefficient of Macho turbulence; C1ɛ, C2ɛ, C3ɛ – fixed values; σk and σɛ – the turbulent Prandtl number for variables k and ɛ, respectively. Sk and Sɛ – variables established by the consumer.
Unlike the enhanced modification (k–ɛ RNG) of the k–ɛ viscosity model, the boundary layer functions are not used, and the model applies to the entire flow area. The employment of the advanced viscosity model, as a rule, requires a more detailed computational grid in the boundary layer and all areas where fluid flow is characterized by decreasing turbulence, i.e. the Reynolds number is small. Using the standard k–ɛ model is sometimes enough, and the alternative may involve the selection of an automatic model in the boundary layer and the consistent details of the computational grid in these zones. The advanced model may achieve a greater accuracy of the results of gas flow distraction and simulating the interaction of multiple gas flows.
The application of the k–ω model assists with solving the system of two nonlinear diffusion equations derived by Wilcox–TKE and a comparative rate of kinetic energy dissipation consisting of equations for turbulent viscosity and shear stress transfer. This viscosity model is widely applied in fluid flows when the Reynolds number, compressibility and discontinuity from the boundary layer are low.
Standard k-ω (Eq. (5) and (6)) and k–ω SST (shear stress transport) (Eq. (5) and (7)) models are expressed by differential equations with partial derivatives [19]:
where Gk – TKE variations under the effect of the average rate gradient; Gω – a variable under the effect of varying ω; Γk and Γω – effective diffusion variables k and ω, respectively where
and
; Yk and Yω – turbulence-induced dissipation variables k and ω, respectively; Sk and Sω – variables established by consumers; Dω – a diffusion variable equal to
; F1 – a fluid mixing function.
The SST–model is a combination of turbulence models k–ɛ and k–ω: the k–ɛ model is applied for assessing the free flow of fluid, and equations for the k–ω model are used for assessing the areas of the boundary layer. The detailed computational grid is required similarly to the cases of k–ω and k–ɛ RNG models.
The research conducted by Menter [19, 20] demonstrated that the application of the k–ω SST turbulent viscosity model was more accurate and reliable for a wider class of the examined fluid flows (particularly when the model encountered inverse pressure gradient flows, aerodynamic surfaces, sudden shock waves) than the standard SST and other SST models.
As for numerical calculations, differential equations are approximated employing the finite volume method that involves the assessment of flow transfer to particulate matter affecting buoyancy forces. The pressure gradient is automatically estimated for calculating the simulation programme only in the case when the value of this force is equal to or is higher than the density of particulate matter.
A detailed and representative computational grid must be used for achieving the reliability and accuracy of the results of the numerical model. For this purpose, three types of the resolution grids of the model for the multi-channel cyclone were formed employing the ANSYS CFD Fluent software package. The grid consists of tetrahedra the length of the edge of which makes no more than 20 mm and the proximity of the formed elements of the computational grid is at least 50 μm. The height of the boundary layer is 0,1 mm. The grid of the boundary area consists of 8 layers. All three computational grids were made by doubling the size (4,440,299; 8,880,597 and 17,761,194). In additional, the mesh structure was defined according to the geometry of the cyclone. The parameters such as proximity settings, inflation parameters and others were adjusted in order to obtain the satisfactory results. In order to create the appropriate mesh near wall the grid elements were reduced there up to 10 times. The medium-accuracy computational grid was selected for the advanced multi-channel cyclone model. The latter case was identified as the most appropriate with reference to the study on the geometry of the multi-channel cyclone [21]. The length of the advanced model for the multi-channel cyclone in different axial directions is as follows: x – 1,600 mm; y – 1,600 mm; z – 3,400 mm (Fig. 1).
The developed numerical model considered the roughness height of the structure of the advanced multi-channel cyclone with secondary gas inlets, which occurred during adhesion and autogenesis processes under gas flow contaminated with aggressive particulate matter.
The roughness height of the model is estimated as a factor having an effect on variations in pressure changes and the exchange of heat and mass in the boundary layer. A modified law-of-the-wall was preferred due to roughness applied to turbulent flows in space terminated with the walls of significant roughness. The degree of roughness is determined by the roughness coefficient (KS+) which, in the case of the smooth surface, does not exceed 2.25 (case 1). Under the semi-smooth surface, its value can be equal to 2.25–90 (case 2). The value of the high-degree roughness height coefficient is greater than 90 (case 3).
Surface smoothness has no effect in case 1, however, its influence increases rapidly in case 2 and particularly in case 3. Thus, the following expressions are used in the software package for each case (8):
where ΔB – the roughness height variable affecting the trajectory of fluid and particulate matter; Cs – the roughness coefficient determining the shape of roughness equal to fine particulate matter making 0.3–0.5; k – turbulent kinetic energy, J; Ks+– the equivalent height of surface roughness, m.
To determine variations in the aggressive gas flow, the case of the inner roughness height of the advanced multi-channel cyclone reaching 0.02 m was selected.
By the default settings, the programme uses the Cs coefficient equal to 0.5 with reference to the turbulence model created in line to the methodology developed by Nikuradse. The methodology assumes that wall roughness is uniform. The coefficients of this model may be adjusted analysing the deposition of coarse grains on the walls or when grains have irregularly shaped large edges.
Motion trajectories of particulate matter have been made using second order solution methods. The track lines of particles of 1 μm, 2.5 μm and 10 μm have been made separately. In a discrete phase model is included: interaction with continuous phase, update DPM (discrete phase model) sources every flow iteration. Maximum number of steps of tracking is equal to 50,000. An injection of particulate matter is released from four inlets at the same time. Particle type is inert and diameter distribution is uniform. The rate of particle is equal to 80% of gas flow velocity and total flow rate is equal to 1e−20 kg/s. A drag law is spherical. Graphic results have been made using particle tracks. It has been used continuous pulse mode and color visualization by particle residence time from 1e−6 s (minimum value) to 1 s (maximum value).
3. The Analysed Results of the Research on the Numerical Simulation of Particulate Matter and Gas Flow ProcessesBased on the research performed by the authors [21], optimal parameters for the computational grid and viscosity model were established thus analysing gas flow processes in the multi-channel cyclone having one installed inlet. With reference to the findings of the study, numerical simulation was extended applying the geometry of the advanced multi-channel cyclone. The settings and adjustment of optimal viscosity models for the examined multi-channel cyclone were built on the minimization of the obtained residuals for the calculated variables of the viscosity model. The case that best corresponded to the results of experimental studies and minimized the residuals of model variables was preferred as optimal to study gas flow processes in the model of the multi-channel cyclone.
For an appropriate selection of the viscosity model, the application of the optimally selected medium-accuracy computational grid was used thus analysing gas flow rate distribution in the channels of the multi-channel cyclone.
Variations in values at the beginning of each channel were analysed in the research on the numerical simulation of gas flow rate distribution. The cross-sectional area positioned 2 cm from the beginning of the edge of the curvilinear element was examined. The analysis was performed in line to 15 research points dividing the total height into 5 and the width of the channel – into 3 sections. The values were fixed at the intersections of the lines separating zones (Fig. 2(a), No. 1).
The calculations made applying subprogram ANSYS 16.1 Fluent demonstrated a graphical representation of the obtained results. Fig. 2 shows the boundary layers of each channel at the peripheral wall (Fig. 2, No. 2). The boundary layer at the outer surface of the quarter-ring element was defined in channel 1 (Fig. 2(a), No. 3) where gas flow was completely stopped. The peaks of gas flow rate occurred at the inner surface of the quarter-ring element, just beyond the boundary layer. The area of this zone was the largest in channel 1 (Fig. 2(a), No. 4), and the values were equal to 15.4–19.5 m/s. As for channel 3, this zone (Fig. 2(c), No. 4) broke approaching the well of the separation chamber, and rate values varied in the range of 11.6–14.5 m/s. In channel 4, the zone of rate peaks was found only between the 1st and 4th curvilinear elements the values of which fluctuated in the range of 12.4–15.7 m/s. In channel 2, the area of this zone was the smallest (less than 20% of the total area between the curvilinear elements), and rates were in the range of 13.1–16.6 m/s.
The obtained results of gas flow rate distribution in the colour palette provided an opportunity to analyse in detail gas flow processes in the advanced multi-channel cyclone. Gas flow in an appropriate outer channel is shown in the section of the separation chamber between the peripheral wall and the curvilinear element (Fig. 2). Each channel has several unique gas flow trajectories and specific rate distribution.
Rates are evenly distributed in channel 1 (Fig. 2(a)) in the middle of which the maximum rates of up to 14.4 m/s prevail. Gas flow does not exceed 1 m/s along the entire boundary layer at the curvilinear element, at the lid of the separation chamber and at the peripheral wall. An area to the convex bottom of the separation chamber may be considered an exception. Gas flow moves toward the outer stretched circular aperture in this zone. Gas flows at a rate of 3.1–5.1 m/s along the well; however, as you approach the curvilinear element, the height of the boundary layer increases, and the rate decreases to 1.0–2.1 m/s in this zone. The reverse flow accelerates, and the values above the circular aperture reach 6.2–9.2 m/s (Fig. 2(a), No. 6). The gas flow trajectory is seen to be directed to the conical hopper of the cyclone. Gas inflow rate at the upper section of the hopper goes down to 2 times and is equal to 3.1–5.1 m/s. This is due to the fact that gas flows through the narrow circular aperture and suddenly enters the space of a large-volume hopper where the kinetic energy of gas flow is quickly suppressed. Such gas flow is conducive to the deposition of particulate matter trapped by the high-rate flow and carried through slits. The particulates next enter the hopper and are not pumped back into the separation chamber due to the low prevailing rate. A part of gas flow enters the hopper via the inner segmental overlapping circular apertures of the channels (Fig. 2(a), No. 7). These slits have a width of 0.005 m and are 6 times smaller than that of the circular aperture. They are arranged in the inner central channel, and therefore only a part of the flow passes through. Gas flow in the cross-section of the slits accelerates to 9.2–11.3 m/s.
Equally to outflow from the circular aperture, gas flow rate decreases abruptly to that predominating in the cyclone in the hopper, i.e. 4.5 m/s on average. The analysis of the obtained results of theoretical (numerical simulation) and experimental studies provided the distribution of gas flow rates in all channels of the cyclone. The comparison of the results with experimental studies is presented in Fig. 3. As a rule, the largest residuals in simulation research are set at the last points examined [22]. For this purpose, gas flow rates at the end of each channel were analysed using an analogous methodology for determining the rate at the beginning of the channel.
The findings of the numerical simulation of the multi-channel cyclone resulted in a conclusion that the smallest computational residuals were obtained only in the case of the low-accuracy computational grid applying the k–ɛ Enhanced Wall Treatment viscosity model. Meanwhile, using medium and high-accuracy computational grids, k–ω SST was optimal. Employing the latter viscosity model together with the medium-accuracy computational grid showed the smallest residuals compared to experimental results, and therefore this case was preferred as optimal and analysed further in this paper. For simulating SFD processes, the optimal k–ω SST viscosity model has been established in the advanced multi-channel cyclone. The application of the 1st and 2nd order discretization equations and optimal relaxation coefficients lead to rate and TKE residuals equal to 10−4, and the residual of the energy variable equalled 10−7.
The analysis of the research findings of experimental and numerical simulation was performed by assessing gas flow rates in four channels of the advanced multi-channel cyclone. The calculated residual values disclosed that gas flow rate values obtained from different studies varied at least at the beginning of each channel and at the end of channel 1. In these cases, relative residuals fluctuate in the range of 4.3–1.8%. Meanwhile, the analysis of gas flow rate in all channels shows variations in the values from 17.6 to 11.8%. Research on numerical simulation applying the geometry of the primary multi-channel cyclone and analysing gas flow processes demonstrated that the medium-accuracy computational grid was an optimal option and resulted in significantly smaller residuals compared to other cases. Then, at the beginning of all four channels, the values differ by only −2.24–8.89%. Therefore, numerical simulation applying the geometry of the advanced multi-channel cyclone was performed using the medium-accuracy computational grid. Also, at the end of all four channels of the multi-channel cyclone, the values determined by simulation were found to be lower than those obtained experimentally, and residuals varied in the range of 6.04–21.49%. The analysis of the findings of the advanced multi-channel cyclone showed that gas flow rate values set by simulation were higher than those of experimental studies only at the beginning of each channels except for channel 1. The relative residual of the last outer channel 4 was the smallest between the results, and the average residual of analysing gas flow rate in all three channels was equal to 8.6%.
A comparison of the research findings of experimental and numerical simulation is presented in Table 1.
A comparison of gas flow rate values showed that close relative residuals averaging 15.4% were established by simulation in the middle of all four channels. Also, in all cases, a lower gas flow rate was obtained compared to experimental studies. A similar trend was observed at the end of channels 2 and 4 when the average relative residual made 15%. Thus, it can be assumed that the established residuals were caused by possible residuals in the geometry model of the advanced multi-channel cyclone, which formed a part of residuals between experimental and simulation research findings of numerical simulation. On the other hand, the residuals of equipment, measurement method and meter influenced the received values in the course of experimental studies as presented in research analysis.
Statistical analysis showed that the mean residual of all modules of values was 12.1%, whereas having estimated positive and negative residuals, it made 7.8%. A strong correlation was found between all values, and the correlation coefficient was equal to 0.96. Having considered all above mentioned factors, it can be concluded that gas flow rate distribution received employing the numerical simulation method in the advanced multi-channel cyclone has been performed in a proper manner, despite the complexity of object geometry and the intricacy of dynamic processes taking place in the examined aggressive gas flow. Nevertheless, the reliability of the results obtained is high enough. As for ongoing research, the received small residuals may be further reduced by making additional assumptions in the model, introducing corrections or additional variables and transferring physical model-specific parameters to the numerical model.
The analysis of gas flow rates in the channels of the cyclone disclosed that the smallest residuals were obtained comparing research findings in channel 1. The mean relative residual reached 6.3%. The obtained research findings showed that the residuals of gas flow rate values increased in channel 2 and the subsequent channels. The difference between experimental and simulation research findings in channel 2 was 2 m/s (absolute residual) and the relative residual made 13.7%. As for channels 3 and 4, the relative residual was equal to 14.9% and 16.5%, respectively. The average relative residual of the analysed research findings was 12.8%. Thus, it can be concluded that the developed numerical model for gas flow in the cyclone is suitable for simulating variations in gas flow rate thus achieving a sufficiently high accuracy (average residual is less than 15%). However, determining gas flow rate has been found to be complex and less accurate in channels 3 and 4 of the cyclone with residuals of 15% or more. It is assumed that such distribution of research findings was influenced by complex varying fluctuations in dynamic parameters, the rate of changes of which increased from the gas flow inlet to the outlet of the cyclone. The combinations and redistributions of multiple gas flows create additional residuals in direct experimental studies. As for numerical simulation, the model solution becomes more and more complex, and therefore additional assumptions are made, which causes additional residuals (Table 1).
For analysing gas flow processes, numerical simulation was performed thus establishing gas flow rate distribution at different heights of the multi-channel cyclone (Fig. 4). Section planes made at the height of 5, 15 and 25 cm and the spectral representation of gas flow rate values in the separation chamber of the cyclone and in the primary and secondary gas flow inlets were provided (Fig. 4(d)). For compiling the numerical model, the parameters describing the rate of aggressive gas inflow at each of gas flow inlets were introduced with reference to the results of experimental studies. Thus, the obtained distribution proves that the maximum rate of gas inflow is observed at the primary inlet where values reached 13.1–14.1 m/s at a height of 15 cm (Fig. 4(d), No. 1). Meanwhile, at the height of 5 and 25 cm from the well of the separation chamber, rates made 12.6 m/s (Fig. 4(d), No. 2). No significant differences were observed in secondary gas flow inlets, and the average rate, e.g. at point No 3 (Fig. 4(d)), was equal to 8,1 m/s. The reason for this distribution has already been extensively analysed during experimental studies.
The analysis of gas flow processes in the advanced multi-channel cyclone demonstrated that the part of gas flow that turned through the outer stretched peripheral slit into hoppers largely entered the upper section of the conical hopper seen in the vertical section (Fig. 4(a)) and its detailed presentation (Fig. 4(e)). For developing the physical model, an attempt was made to install a slit of an appropriate width (a slit 3 cm wide was preferred) to effectively deposit particulate matter moving in the aggressive gas flow. Gas inflow through the slit was found to be 9 m/s (Fig. 4(e), No. 5) and decreased to 5–6 m/s at a radius of 5 cm from the peripheral wall (Point No 6). In the middle of the section between the peripheral wall and the axis of the cyclone, the rate was 2–3 m/s (Point No 7) and that in the axis of the cyclone – 0–1 m/s (Point No. 8).
Gas flow rate was established to vary strongly in the section of the hopper at the peripheral slit to the section where inner segmental circular overlapping apertures of the channels were installed. At the next stage, when moving towards the axis of the cyclone, the distances between the isolines of different values increased, and the sections were arranged as vertical planes, i.e. a sudden drop in the rate in the direction of the axis of the cyclone. Such gas flow suppression facilitates the prevention of taking back particulate matter to the separation chamber due to high velocity vortices or pumping under the operation of the multi-channel cyclone for removing dust from gas flow.
The calculated numerical model provides that considering all four outer channels of the cyclone, the maximum gas flow rate was determined in channels 1 and 2. The gas flow rate increases at the end of these channels in particular, and values rise up to 14.1–17.1 m/s (Fig. 4(b), Point 9). Fig. 4(d) shows that the trajectories of the maximum gas flow rate move only in the middle of the cross-section of the channel, whereas approaching the walls the rate decreases sharply and does not exceed 5 m/s (Point No. 10). In channel 3 of the cyclone, gas flow rate varies slightly, the average value is in the range of 8.0–10.1 m/s and decreases by approximately 20% at a height of 5 cm from the well of the separation chamber, i.e. values range within the interval from 5.0 to 8.0 m/s. In the lower section of the middle of channel 4 arranged 5 cm from the well of the separation chamber, gas flow rate was found to decrease the most, and values did not exceed 6 m/s. Thus, it can be concluded that the reason for this phenomenon is twofold: the loss of the kinetic energy of gas flow through the channels of the cyclone and an increase in the cross-section of channel 4 of the cyclone.
To describe vertical distribution, a double section of the plane was selected: the first plane intersected the beginning of channel 1 passing through the axis of the device and intersecting the beginning of channel 3 at the end; the second plane intersected the beginning of channel 2 and the beginning of channel 4 in the end (Fig. 4(a)). With reference to the obtained isolines, gas flow velocity in the hopper of the cyclone decreased from 8 m/s (Fig. 4a, No 11) to 1.0 m/s (Fig. 4(a), No 7). The zone of the lowest gas flow rate in the advanced multi-channel cyclone is situated in the axis of the upper conical section of the hopper (Fig. 4(a), No 8) and in the entire lower conical section of the hopper (Fig. 4(a), No 12) where gas flow rate does not exceed 1.0 m/s. The zone of the lowest gas flow rate of the hopper is distributed at approximately 0.1 m on both sides from of the axis of the device. The low gas flow rate in the hopper of the cyclone plays an important role, because an inflow of particulate matter to the hopper will not be taken back to the separation chamber, which will increase treatment effectiveness [23].
The gas flow outlet and duct are installed in the upper section of the separation chamber along the axial line of the multi-channel cyclone. Gas flow reaches a rate of 19.1–20.1 m/s in this zone (Fig. 4(a), No 13) immediately after entering the gas flow outlet duct.
The numerical simulation of gas flow processes was performed to determine parameters for static pressure and TKE at the walls of the advanced multi-channel cyclone. These parameters are important for analysing gas flow due to the applied dynamic forces and their interaction with the inner elements of the cyclone (Fig. 5).
Research on gas flow static pressure distribution in the advanced multi-channel cyclone has identified the areas where gas flow has the greatest effect on the walls of the device thus having the highest potential energy. The assessment of the static pressure distribution spectrum (Fig. 5(a)) demonstrates that values reach 567–607 Pa (Fig. 5(a), No 1) at the beginning of the primary and secondary gas inlets. However, this value remains until the beginning of the channel in the first inlet only, then decreases to 548 Pa and finally recovers to the value of 587 Pa. Static pressure decreases to 528–567 Pa at the locations of the third and fourth gas inlets of the respective channels, and the zone of such pressure stretches throughout channels 3 and 4 (Fig. 5(a), No 2). In the middle of each channel, except for channel 4 (Fig. 5(a), No 3), a static pressure drop zone is formed at the installed folded plate. The area of the zone is the largest in channel 1 and is spread over the entire width of channel 1 where pressure is equal to 548 Pa. As for channels 2 and 3, the area of lower static pressure occupies only a small part closer to the folded plate where pressure is equal to 509 Pa.
The distribution of static pressure in the inner central channel differs significantly from the situation in the outer channels. First, pressure values are distributed in the range of 293–450 Pa in this channel, which indicates a suppressive gas flow compared to outer channels. A large difference between the highest and lowest value may be the result of high-rate gas flows in the outer channels suddenly entering the inner channel. Due to the motion trajectory around the central axis of the device, gas flow causes variations in pressure throughout the central channel. Thus, static pressure in the gaps between curvilinear quarter-rings changes several times. The initial pressure of approaching the inlet to the gap is 548 Pa (Fig. 5(c), No 7). Further, the static pressure of the flow decreases from 528 Pa to 371 Pa until it reaches the inter-ring zone (Fig. 5(c), No 8). As for the area between curvilinear elements, static pressure is equal to 332–371 Pa (Fig. 5(c), No 9), which increases again to 390 Pa when it enters the inner central channel (Fig. 5(c), No 10).
Variations in the static pressure of gas flow in the axis of the advanced multi-channel cyclone and in the gas flow outlet duct are given in detail (Fig. 5(b)). Three main areas can be distinguished: the first area is situated 5 cm from the wall of the gas outlet duct at a pressure of 332–371 Pa; the second area is a boundary layer (edge) with the gas outlet duct at pressure equal to 214–253 Pa; the third area is the gas flow outlet duct where the value of static pressure makes 81 Pa. The latter area faces the largest pressure drop throughout the entire advanced multi-channel cyclone, and gas flow moves from the inner central gas channel to the gas outlet duct. Next, gas flows along the outlet duct, and static pressure increases slightly to 18–57 Pa.
Variations in static pressure below the well of the separation chamber are not analysed in detail, because the pressure of both parts of the conical hopper coincides and is equal to 543 Pa on average (Fig. 5(a), No 2).
The computational dynamics of fluids is based on the application of the iterative method to obtain variables – the values of parameters for rate components, pressure, energy, etc. and distribution in the examined field subject to boundary conditions describing the specific objective.
The conducted research examined the flow of aggressive gas and the motion processes of this flow in the advanced multi-channel cyclone. Modifications to the optimally adapted viscosity models are based on TKE parameter (k) the residuals of which were examined in conjunction with other variables. Research on static pressure defines the potential energy of gas flow in the investigated ‘channel’, and parameter k explains energy transfer of the turbulent (pulsating) gas flow. To analyse the obtained difference, TKE parameter distribution was made in the advanced multi-channel cyclone (Fig. 6).
For analysing TKE parameter, the spectral distribution of the complete structure of the advanced multi-channel cyclone (Fig. 6(a)) and at the inlet to the gas flow outlet duct (Fig. 6b) was formed. Also, the details of gas flow processes in the gaps between curvilinear quarte-rings were given (Fig. 6(c)–(f)).
The value of TKE ranged within the interval from 1.46·10−7 m2/s2 to 17 m2/s2. Despite a wide range of values, most of the advanced cyclone falls into the bluish spectrum that corresponds values from 1.7 m2/s2 to 4.25 m2/s2. The lowest values are set at the beginning of each gas flow inlet, e.g. Fig. 6(a), No 1 where values do not exceed 0.85 m2/s2. Thus, the flow is little turbulent in these areas, close to the direct current, and variations in kinetic energy change insignificantly. The area defined at the beginning of each channel runs the full height of the channel. In this section, the value of TKE is equal to 1.7–2.6 m2/s2. Following the first inflow, this area was found to be the largest, following the second, it became smaller, etc. It may be concluded this is influenced by inlet rate, which, in this case, is the highest in the first inlet and decreases in each subsequent inlet. Gas flow rate affects flow turbulence and hence TKE.
The highest value of TKE has been set in the inner central channel, at the inlet from the separation chamber to the gas flow outlet duct. The largest value has been set at point 2 (Fig. 6(b)) and is equal to 17 m2/s2. This can be attributed to vortex motion and intense mixing in the central channel. Also, the flow pumped at the axis of the device to the gas duct of a smaller cross-section, i.e. the gas flow outlet duct, has a profound effect compared to the inner central gas duct. For the overall assessment of the central channel, the value of TKE reaches 3.8 m2/s2. However, at the inner surface of each quarter-ring element, the established values make 1.5·10−7 m2/s2. These zones are supposed to fully confine to bordering areas where no gas flow is observed or motion is very weak.
Curvilinear quarter-rings are one of the most important areas of the multi-channel. The gaps between the arranged elements divide gas flow into the peripheral and transit flow. TKE distributions were observed in all four areas between the gaps of adjacent curvilinear elements (Fig. 6(c)–(f)). The analysis of these zones led to the conclusion that the largest areas having the highest values were set at two sites. The first site was found in the gap between the 1st and 4th curvilinear quarter-ring elements at the inner edge of the 1st element when gas flew in the transit direction to the central channel (Fig. 6(c)). The other site was the gap between the 3rd and 4th curvilinear elements at the inner edge of the 3rd element when gas flew in the reverse peripheral direction from the central channel to outer channel 4 (Fig. 6(f)). In both cases, the values of TKE ranged from 10.2–11.1 m2/s2 in the middle of the gaps. A similar trend was observed in the gaps between other curvilinear elements (Fig. 6(d) and (e)) when gas flow deviated in the peripheral direction and a vortex formed at the edge of the previous curvilinear element (Fig. 6. No 3). In these cases, the average value was 13.2 m2/s2, but in the first case (Fig. 6(d)), the area was larger due to turbulent motion. The values of TKE decreased to 8.5 m2/s2 when the flow entered the area limited to the surface of a single curvilinear element, e.g. Fig. 6(d), No 4.
Only a few areas at the level of 0.1–0.15 m below the well of the separation chamber at the end of each channel of the cyclone were observed in the conical hopper of the multi-channel cyclone. The largest value in these sections of the hopper reached 6 m2/s2, and the average was equal to 1.3 m2/s2. The values decrease to the lowest one set in the model below this area, including the lower section of the hopper, and therefore analysis does not apply to these areas.
The effective deposition of particulate matter in the advanced multi-channel cyclone is influenced by the analysis of aggressive gas and particulate matter motion processes. For this purpose, particulate matter motion trajectories from their inlet to deposition in the hopper or to removal through the outlet duct of the treated gas flow have been investigated. The cases of the average diameter of particulate matter in aggressive gas inflow equal to 1 μm, 2.5 μm, 10 μm, and 70 μm have been examined (Fig. 7).
For analysing the finest selected particulate matter of 1 μm in diameter, a path of particulate matter trajectories was formed in the advanced multi-channel cyclone (Fig. 7(a)). The colour of the trajectory line describes time taken for the particulate to reach the examined point. Fig. 6(a) shows the even inflow of particulate matter into all channels of the cyclone over a period not exceeding 5 s. Once in the separation chamber, approximately 20% of particulate matter immediately enter the upper section of the conical hopper through a peripheral slit. Along with the vortex, the trajectory of particulate matter descends toward the junction of two sections of the conical hopper thus entering the lower section of the conical hopper. A particulate reaches this place within 11.9 s after inflow and persists up to 47.7–71.5 s. The particle is then trapped by the vortex, redirected towards the separation chamber, enters the central channel and is pumped into the gas outlet duct following 119 s.
Under industrial conditions, reversing particulate matter to the separation chamber will be avoided, as closure is usually installed in the lower section of the hopper, and an endlessly operating device discharging the hopper removes all accumulated particulate matter. The effectiveness of trapping extremely fine particulate matter may be increased by installing a pump that is forced to extract gas flow together with the trapped particulate matter. In line to the calculations provided by numerical simulation, the trapped particulate matter accounted for 22.3% of the total content of particulate matter inflow to the advanced multi-channel cyclone. Compared to the results of experimental studies, the obtained average particulate matter removal effectiveness was by 4.1% lower (Fig. 3).
The process of removing the particulates of 2.5 μm to 10 μm present in aggressive gas from the flow is mostly relevant to the studies of the advanced multi-channel cyclone. Conventional cyclones are hardly effective for trapping particulate matter, and industrial emissions increasingly contain the particulate matter of such diameter. The findings of the performed numerical simulation studies analysing the trajectory of particulate matter of 2.5 μm in diameter are presented in Fig. 6(b), and those of particulates of 10 μm – in Fig. 6(c). Particulate matter trajectories and travel time from inflow to the inlet to the channels of the cyclone are similar to the case of examining particulate matter of 1 μm in diameter. The flow of particulate matter of 2.5 μm and 10 μm in diameter in the channels is similar because trajectories are circular and descending towards the well of the separation chamber. Particulate matter of 2.5 μm in diameter enters the upper section of the conical hopper only through the peripheral slit, while approximately 20% of particulate matter of 10 μm in diameter flow through the inner segmental slits of the channels. Also, time for particulate matter of 2.5 μm in diameter to reach the conical hopper is equal to 0.4–0.55 s, whereas time for particulates of 10 μm makes 0.45–0.75 s.
Due to heavier weight, particulate matter of 10 μm in diameter tends to remain in the separation chamber for a longer time, which is up to 0.9 s, while around 30% of particulate matter is removed together with gas outflow, and the rest re–enters the hopper through slits to survive. The complete precipitation process takes on average approximately 1 second. However, some major differences between the sizes of these types of particulate matter are noticed. The first difference reflects particulate matter removed through the gas flow outlet duct mostly along the peripheral wall and then abruptly lifted by the flow and pumped into the gas duct. Larger particulate matter of 10 μm in diameter enters the gas flow outlet duct, moves via the channels of the cyclone, enters the inner central channel together with the peripheral flow, approaches the axis of the cyclone and then is vortexed and removed from the separation chamber with gas flow. The reason for such processes may be considered gas flow moving away from the axis of the device and not able to transfer larger particulate matter; however, such flow manages to transfer fine, for example, 2.5 μm in diameter and finer particulate matter. The motion of vortex flow in the axis of the advanced cyclone is of a rising trajectory and contains high kinetic energy. Thus, such flow manages to transfer, lift and remove particulate matter of 10 μm in diameter. The findings of the study of particulate matter flow showed that the effectiveness of trapping particulate matter of 10 μm in diameter was on average 1.7 times higher and made 71.9% than that of the particulates of 2.5 μm in diameter trapped at the effectiveness of 41.3%. Compared to the results of experimental studies, the larger is the diameter of particulate matter, the smaller is the residual between the conducted studies. Experimentally, an average trapping effectiveness of 46.9% and 78% for particulate matter of 2.5 μm and 10 μm in diameter, respectively was obtained (Fig. 3). The made calculations demonstrated that, in all cases, the effectiveness of trapping particulate matter was estimated to be lower than that obtained experimentally with a mean residual of 11.8%.
Verification of the simulation results with the results obtained experimentally showed that the obtained gas flow rate values differ by 12.8%. Although, the results of the effectiveness of removing particulate matter showed that the difference between the values obtained in the experimental studies is smaller than the gas flow rate. The difference between the results of the removal efficiency of the smallest 1 μm diameter particles was equal to 4.1%, 12% – for particles of 2.5 μm diameter, and 7.8% – for the largest particles of 10 μm diameter.
A gas flow and particle motion were determined by the gas dynamics of the physical model and the geometry of the cyclone. The numerical model was identically developed based on the prototype of the experimental bench. The k-ɛ viscosity model was improved by the values of physical parameters that were determined experimentally.
In addition to the analysis of fine-dispersed particulate matter, the performed numerical simulation determined the critical diameter of the particulate, which assisted in trapping all particulate matter in the hopper. The inflow of aggressive gas together with particulate matter of 70 μm in diameter found that no particulates entered the gas flow outlet duct. Trapping all particulate matter did not exceed the time of 1 s. The generated profiles show that immediately after inflow into the channels of the advanced multi-channel cyclone, the trajectory line of particulate matter was descending and particulate inflow through the outer continuous peripheral slit entered the conical hopper of the upper section within a period of 0.6–0.85 seconds. Following approximately 0.1–0.2 s, the inflow of all particulate matter moved from the upper to the lower section of the hopper. The effectiveness of trapping particulate matter of 70 μm in diameter was assessed and made 99.4%. Thus, it is assumed that the rest can be considered as a systematic residual, i.e. the numerical simulation program estimated particulate matter as injected in conjunction with the aggressive gas flow rather than through the inlet or trapped in the hopper.
4. ConclusionsThe paper has applied to ANSYS Fluent software to numerically simulate particulate matter dynamics and gas flow processes. The cases of using the modified SST k-omega viscosity model were analyzed to investigate the aggressive gas-particulate matter flows in the new modified multi-channel cyclone. The main conclusions are summarized as follows:
Firstly, the zones of the expected adhesion are located along the peripheral wall and at the outer surface of the quarter-ring element, where the gas flow rate does not exceed 1.6 m/s. Strong vortex flows having an adverse effect on deposition effectiveness occur at the outer surface of the inner quarter-ring element beyond the boundary layer where the maximum gas flow rate reaches 13.6–16 m/s. In this case, experimental studies have found that the maximum gas flow rate is 17.6 m/s, i.e. the relative residual does not exceed 9%.
Secondly, numerical simulation has disclosed that the static pressure zone of the maximum gas flow is at the inlet duct of the cyclone and at the beginning of the first channel where pressure values reach 310–336 Pa. Due to such pressure distribution, the motion trajectory of particulate matter of a relatively small diameter (1–2.5 μm) coincides with the trajectory of gas flow (particulates move together with the gas flow), i.e. directed towards the axis of the cyclone and deposited less efficiently compared to particulate matter of 10 μm in diameter. Experimental studies have proved that the static pressure of gas flow reaches 640 Pa prior to entering the cyclone but decreases by 50% in the section up to channel 2. Intense mixing of flows has been noticed opposite to each edge of the curvilinear element at approximately 50 mm, which triggers the filtration process of the new more polluted flow, and the values of static pressure range between 162 and 216 Pa.
Thirdly, the effectiveness of removing particulate matter of 2.5 μm and 10 μm in diameter in the advanced multi-channel cyclone were 71.9% and 41.3%, respectively. Relatively all particulate matter exceeding the diameter of 70 μm is trapped. The difference between the results obtained and experimental studies is less than 15% and equals to 11.8%.
Finally, a good agreement is obtained between the numerical and the experimental results. An error of gas flow rate is equal to 12.8%, the average error of effectiveness of removing particulate matter of 1 μm, 2.5 μm and 10 μm is less than 8%. Concerning the results of numerical simulation, using the Fluent subprogram of the ANSYS software package and applying a different number of volumetric elements assisted in obtaining the smallest residuals of model variables under the employed modifications of viscosity models k–ɛ and k–ω. To achieve greater computational accuracy, the digital cyclone model consisting of 8.88M volumetric elements has been developed thus expanding the computational grid and including 8-stair stepping to form the boundary zone. Independent grids have been created for inlet and outlet channels.
NotesAuthor Contributions P.B. (Professor) reviewed the manuscript and provided valuable insights. A.C. (Professor) developed the conceptualization, methodology and provided valuable research insights. T.L. (Assistant Professor) designed and wrote the original draft of the manuscript, provided valuable insights and helped to review the manuscript. A.C. (Ph.D.) developed the conceptualization, methodology, provided literature resources and analysis, wrote the manuscript and helped to review the manuscript. All authors read and approved the final version of the manuscript. References1. Wasilewski M, Brar LS. Optimization of the geometry of cyclone separators used in clinker burning process: A case study. Powder Technol. 2017;313:293–302.
2. Shilyaev MI, Shilyaev AM. Relationship between the energy and fractional methods for designing wet-type collectors. Theor Found Chem Eng. 2005;39:555–560.
3. Zhao B, Su Y, Zhang J. Simulation of gas flow pattern and separation efficiency in cyclone with configurational single and spiral double inlet configuration. Chem Eng Res Des. 2006;84:1158–1165.
4. Fassani FL, Goldstein L. A study of the effect of high inlet solids loading on a cyclone separator pressure drop and collection efficiency. Powder Technol. 2000;107:60–65.
5. Elsayed K, Lacor C. The effect of cyclone vortex finder dimensions on the flow pattern and performance using LES. Comput Fluids. 2013;71:224–239.
6. Brar LS, Sharma RP, Dwivedi R. Effect of Vortex Finder Diameter on Flow Field and Collection Efficiency of Cyclone Separators. Particul Sci Technol. 2014;33:34–40.
7. Brar LS, Sharma RP, Elsayed K. The effect of the cyclone length on the performance of Stairmand high-efficiency cyclone. Powder Technol. 2015;286:668–677.
8. Elsayed K, Lacor C. Numerical modeling of the flow field and performance in cyclones of different cone-tip diameters. Comput Fluids. 2011;51:348–359.
9. Brar LS, Elsayed K. Analysis and optimization of multi-inlet gas cyclones using large eddysimulation and artificial neural network. Powder Technol. 2017;311:465–483.
10. Misiulia D, Andersson AG, Lundström TS. Computational Investigation of an Industrial Cyclone Separator with Helical-Roof Inlet. Chem Eng Technol. 2015;38(8)1425–1434.
11. Brar LS, Sharma RP. Effect of varying diameter on the performance of industrial scale gas cyclone dust separators. Mater Today: Proceedings. 2015;2(4–5)3230–3237.
12. Elsayed K, Lacor C. The effect of cyclone inlet dimensions on the flow pattern and performance. Appl Math Model. 2011;35:1952–1968.
13. Sommerfeld M, Ho CH. Numerical calculation of particle transport in tur-bulent wall bounded flows. Powder Technol. 2003;131:1–6.
14. Zhou Z, Wang G, Chen B, Guo L, Wang Y. Evaluation of Evaporation Models for Single Moving Droplet with a High Evaporation Rate. Powder Technol. 2013;240:95–102.
15. Muschelknautz E, Trefz M. Pressure loss and degree of absorbency in cyclone [Druсkverlust and Absheidengrad in Cyclon]. VDI Warmenatlas. 2006;6:1–8.
16. Santana JDAM, Arnosti S, Coury JR. Performance of Cylindrical-conical cyclone with different geometrical configurations. Braz J Chem Eng. 2001;18(3)1–14.
17. Naik B, Khatua KK, Wright N, Sleigh A, Singh P. Numerical modeling of converging compound channel flow. ISH J Hydraul Eng. 2018;24(3)285–297.
18. Ansys. Support and documentation for customer. Release 18.0. SAS IP. 2017;
19. Menter FR. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994;32(8)1598–1605.
20. Menter FR. Review of the SST Turbulence Model Experience from an Industrial Perspective. Int J Comut Fluid Dyn. 2009;23(4)305–316.
21. Baltrėnas P, Chlebnikovas A. Removal of fine solid particles in aggressive gas flows in a newly designed multi-channel cyclone. Powder Technol. 2019;356:480–492.
Fig. 1The geometry and computational grid of the advanced multi-channel cyclone with secondary gas inlets: (a) – general view of the object; (b) – 1, 2, 3, 4 – cross-section at the beginning of channels 1, 2, 3 and 4 of the advanced cyclone, respectively; (c) – general view of the grid of the object at the vertical section; (d) - connection of primary and secondary gas inlets to the separation chamber and a compacted grid of quarter-ring elements and the adjacent slits of inner channels. 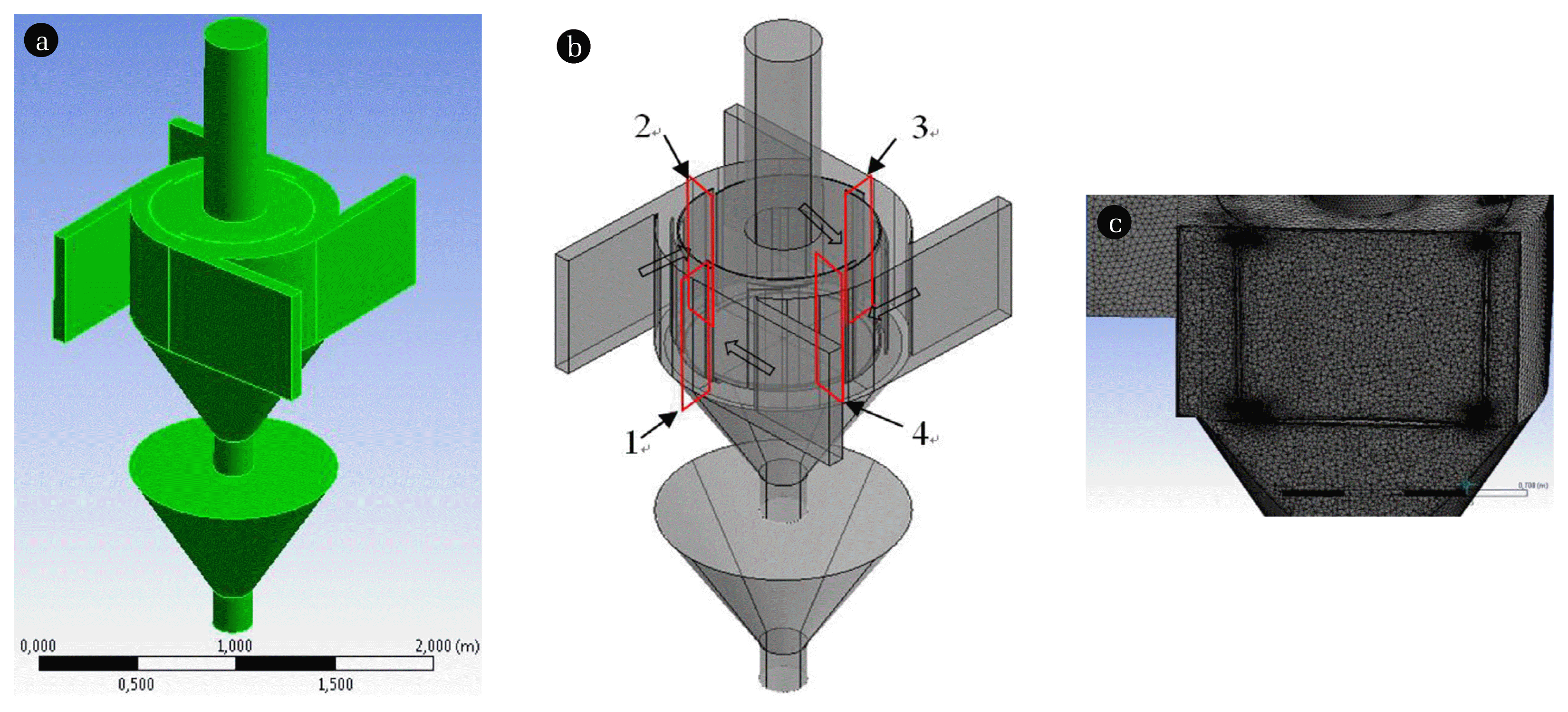
Fig. 2Gas flow rate distribution in the numerical model of the advanced multi-channel cyclone in channels 1 (a), 2 (b), 3 (c) and 4 (d): 1 – set gas flow rate point in the grid; 2, 3, 4 – bordering layer at the peripheral wall and at the outer and inner surfaces of the quarter-ring element; 5 – adjacent quarter-ring element; 6, 7 – outer stretched circular aperture and inner segmental overlapping circular aperture of the channel; 8 – appropriate outer channel. 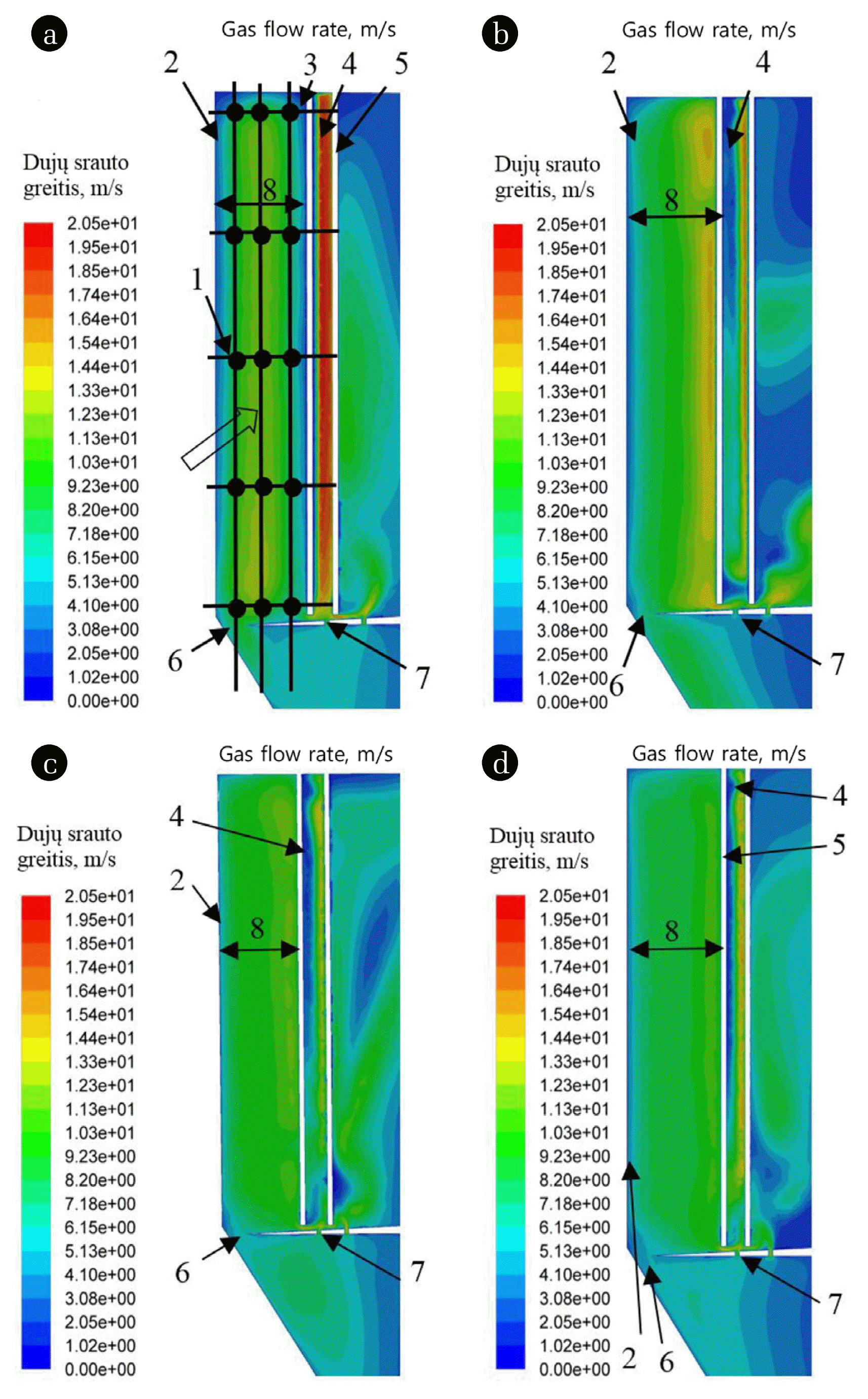
Fig. 3The comparison of the experimental (a) and numerical modelling (b) results of average gas flow rate and particulate matter removal effectiveness of the advanced multi-channel cyclone. 
Fig. 4Gas flow rate distribution: in horizontal sections at the height of 5 cm, 15 cm and 25 cm in the separation chamber of the advanced multi-channel cyclone and on to the planes of the vertical double-section; A–A – variations in the rate on to the horizontal plane 5 cm from the separation chamber at the well level (e); B–B – variations in the rate on to the vertical plane at the section passing through gas flow inlets 1 and 3. 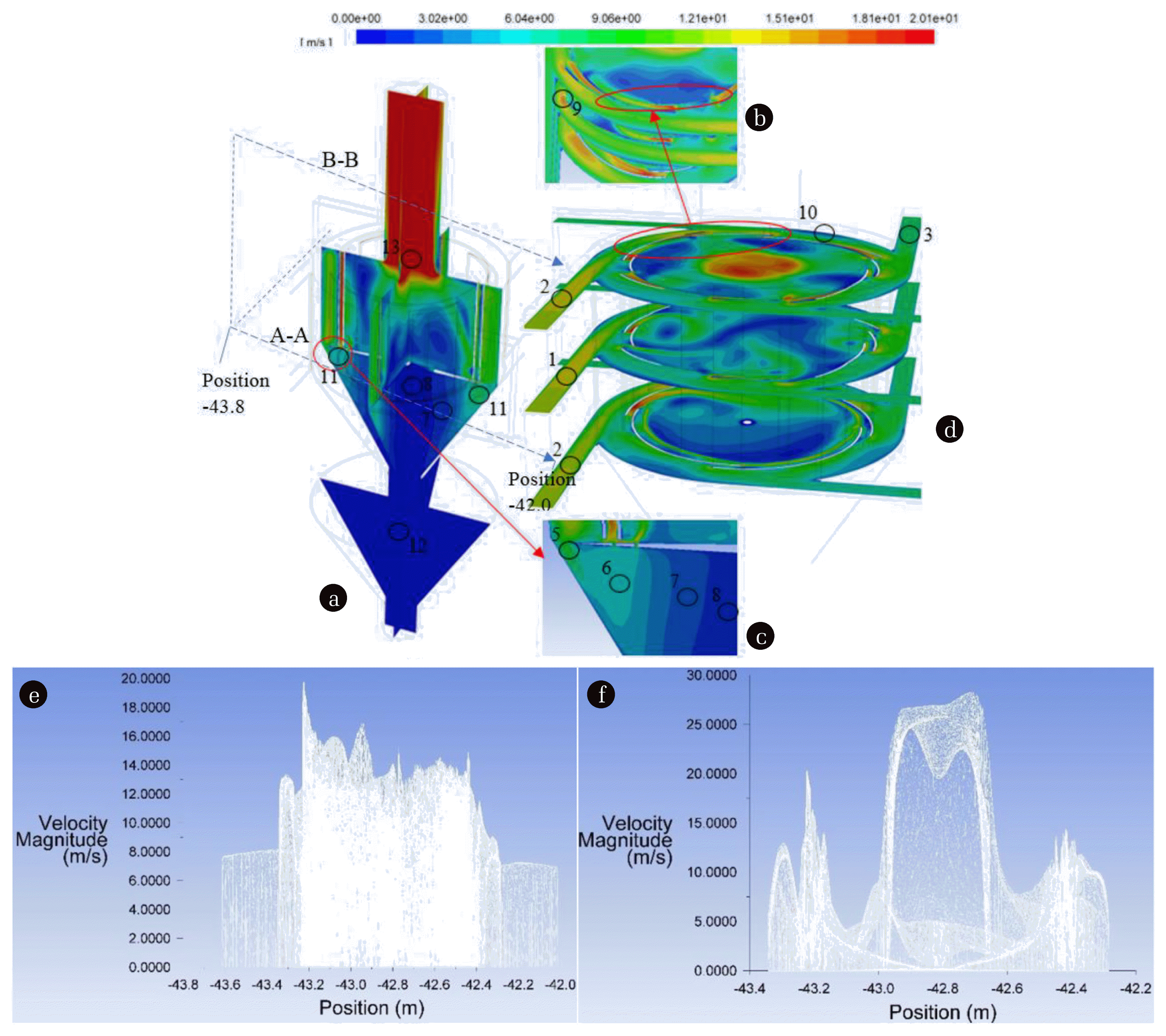
Fig. 5(a) The distribution of gas flow static pressure at the walls of the advanced multi-channel cyclone, (b) the details of variations in static pressure in the gas flow outlet duct (c) and in the gap between curvilinear quarter-ring elements. 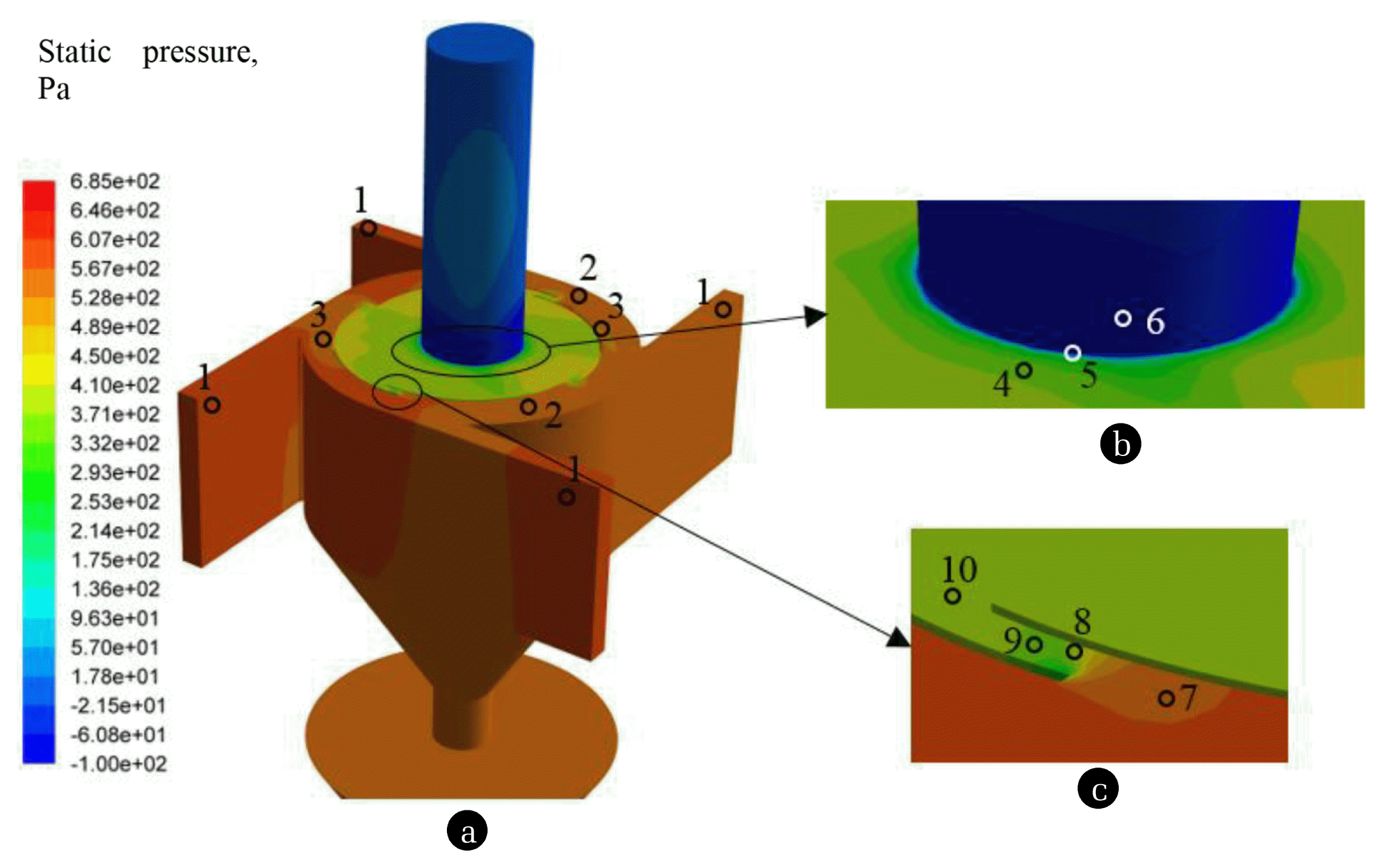
Fig. 6(a) The distribution of turbulent kinetic energy in the aggressive gas flow in the separation chamber at the walls of the advanced multi-channel cyclone, (b) in the gas flow outlet duct, (c)–(f) and in the gaps between the 1st and 4th curvilinear quarter-ring elements. 
Fig. 7The motion trajectories and time of particulate matter of 1 μm, 2.5 μm, 10 μm and 70 μm in diameter in the aggressive gas flow of the advanced multi-channel cyclone applying the modified k–ω SST viscosity model. (a)–(d) Time of particle motions, s. 
Table 1The Relative Residuals of Gas Flow Rate Values in Line to Research on Experimental and Numerical Simulation Conducted in the Channels of the Advanced Multi-Channel Cyclone |
|
|||||||||||||||||||||||||||||||||||||||||