AbstractThis study was aimed at using the Central Composite Design (CCD) and Box-Behnken Design (BBD) to compare the efficiency and to elucidate the main interacting parameters in the upflow anaerobic sludge blanket (UASB) reactor, namely: Organic Loading Rate (OLR), Hydraulic Retention Times (HRT) and pH at a constant temperature of 35°C. Optimum HRT (15 h), OLR (3.5 kg.m−3.d−1) and pH (7) resulted in biogas production of 5,800 mL/d and COD removal of 80.8%. BBD produced a higher desirability efficiency of 94% as compared to the CCD which was 92%. The regression quadratic models developed with high R2 values of 0.961 and 0.978 for both CCD and BBD, respectively, demonstrated that the interaction models could be used to pilot the design space. BBD model developed was more reliable with a higher prediction of biogas production (5,955.4 ± 225.3 mL/d) and COD removal (81.5 ± 1.014%), much close to the experimental results at a 95% confidence level. CCD model predictions was greater in terms of COD removal (82.6 ± 1.06% > 80.8%) and biogas production (4,636.31 mL/d ± 439.81 < 5,800 mL/d) which was less than the experimental results. Therefore, RSM can be adapted for optimizing various wastewater treatment processes.
1. IntroductionWastewater treatment processes are complex, therefore, the incorporation of multiple variables during the treatment process for the optimum performance of the system is necessary. Each of the chosen variables is expected to be operated at an optimum range to maximise the benefit of the process, therefore, optimization becomes very important [1, 2]. In fact, the feasibility of the conventional techniques, such as the one-factor-at-time (OFAT) is very challenging in environmental processes and wastewater treatment systems for acquiring the best conditions to maximise the desired response or treatability performance [1, 3]. Conventionally, the OFAT method which involves changing one independent variable while holding others at fixed level is extremely time consuming and expensive to run high number of experiments. Subsequently, optimization using multivariable techniques is encouraged, as they are economical, faster, and effective to optimize multivariable simultaneously. Furthermore, the multivariable approach offers the advantage of interactive effects among the factors [4].
Consequently, due to the powerful efficiency of the multivariable technique, response surface methodology (RSM) has been encouraged for optimization of various process systems. The RSM is a resourceful tool which is made up of mathematical and statistical techniques that are based on the fit of a polynomial equation to the experimental data in order to predict the behaviour of the system [5]. It has been employed for the optimization of various wastewater treatment processes to improve the water quality [3, 6].
A study by Bashir et al. [7] reported that out of 3,190 articles published within the year 2000 to 2013 (data extracted from Scopus), about 352 documents were related to the application of RSM for process optimization in different subject areas of research. Some of which were engineering (15.6%), biochemistry (11.2%), agricultural and biological science (10.6%), chemical engineering (9.5%) and environmental science (6%) [7, 8]. The studies carried out in the optimization of operational factors in different types of wastewater treatment processes by various authors includes textile dye wastewater [3] landfill leachate [6], oil refinery wastewater [1] and the sugar refinery wastewaters [9].
The RSM has been shown to be advantageous over the traditional techniques of optimization with respect to the number of experiments and multifactor interactions [1]. RSM, as a collection of a mathematical and statistical tool, is usually used in designing of experiments as well as for the evaluation of the most influential factors on chosen responses. This tool describes the interactional effects between a set of data. Again, it can be used to generate models for the prediction of the responses. To expand the application of RSM, there is the need to evaluate which of the design types fit for the number of process parameters. Some of the design types of RSM include Doehlert Design (DD), Central Composite Design (CCD), the Box-Behnken Design (BBD) and a three-level full factorial design [3, 6]. Each of the design types offers both advantages and disadvantages.
To increase the bioremediation efficiency, more especially in UASB systems, it is crucial to know the optimal operating conditions. Since some of the influential parameters in biological systems have interactional effects which can inhibit a shift in microbial community. Bezerra et al. [3] reported that using minimum number of experimental runs, a correlation can be developed to evaluate the relationship between the response of interest and the input variables. Ibrahim, et al [4] used BBD to model and optimize external parameters of biological system for the removal of COD and phosphorus. The results showed that at optimum temperature of 45.33°C and 60 d, desirability performance of 99.8% was obtained for the removal of COD and phosphorus, which correspond to 95% confidence at index R2 of 0.955 and 0.91, respectively. Amr et al [10] conducted a study on three independent factors (ozone dosage, COD concentration, and reaction time) using RSM to evaluate the treatment of semi-aerobic stabilized leachate. The obtained optimum conditions were 70 g/m3 ozone, 250 mg/L COD, and 60 min reaction time for 26.7, 7.1, and 92% removal for COD, NH3–N, and colour, respectively.
The use of RSM as an optimization tool is seen to be increasing as earlier indicated by Bashir et al. [7], little information for its application in biological wastewater treatment systems exist. Biological wastewater treatment systems such as the upflow anaerobic sludge blanket (UASB) are preferred for the treatment of wastewaters with high organics such as those from the slaughterhouses due to their robustness. The incomplete removal of organic matters and pathogens is one of the disadvantages of the UASB reactor [11, 12]. The performance of the UASB is easily affected by both environmental and operational factors. Therefore, to improve the efficiency of a UASB processes, it is expected that the operational parameters are operated at an optimum. The optimization of UASB processes has been carried out mostly with the use of OFAT which does not consider the interactional effects on the response. The use of RSM for the optimization of both input variables either independently or in combination will be necessary.
The information with regards to the comparative modelling and optimization of biogas production and COD removal efficiency in an UASB process is limited. A few studies have attempted to model and optimize UASB processes using one of the optimization tools, but very little or none have looked at the comparison of both optimization tools [1, 9, 13, 14]. The present study therefore focused on simulating and comparing the CCD and BBD response surface designs to evaluate their desirability efficiency in a biological wastewater treatment process. In this study, the effects of the HRT, pH and Organic Loading Rate (OLR) as independent parameters of UASB for the breaking down of the organic and inorganic components such as the COD to generate the biogas was investigated. Statistically designed RSM were used to optimize the aforementioned parameters at different levels and understand their interactive effects on the responses (COD and biogas) at maximum target. These two parameters were chosen due to the fact that the treatment efficiency is mainly influenced by them.
2. Materials and Methods2.1. Synthetic WastewaterA 25 L synthetic wastewater was prepared before each experimental run. The wastewater was characterized according to specification by Lettinga and Pol [15] with a Biological Oxygen Demand (BOD)/COD ratio of 0.40–0.53 comparable to slaughterhouse wastewater. The synthetic wastewater was continuously fed into a 5 L UASB at the flowrate predetermined by a peristatic pump (Flexflo A-100E, Blue-White Industries Ltd.).
2.2. Seed sludge and Experimental ApparatusThe UASB reactor used for the experiment was constructed from plexiglas glass and its effective working volume was 4.5 L. The UASB was continuously fed with synthetic wastewater at the bottom of the reactor and the effluent was collected at the top. It was operated at a constant mesophilic temperature of 35 ± 1°C. Fig. S7 shows a schematic diagram for the experimental set-up. The reactor was started with a TSS of 19.4 g/L and VSS of 13.8 g/L digested seed sludge collected from a local wastewater treatment plant treating slaughterhouse wastewater in South Africa. The pH of the reactor was maintained by the addition of 1 M HCl and 1 M NaOH. Table S3 shows the characteristics of the wastewater that was used for the experiments. The performance of the reactor was calculated using Eq. (1).
Where, CODout = Effluent and CODin = Influent
The reactor was started with an OLR of 1.54 kg.m−3.d−1 at a HRT of 24 h for the first three days of the start-up where it was operated in a batch mode, thereafter, the continuous mode was used. The OLR was thereafter increased in a stepwise manner according to the chosen HRT (6, 12 and 18 h) and it was maintained to enable the microorganisms to adapt to the new loadings until the system had attained stability. Upon HRT change, the reactor was run for a period of 50 d before changing to the next.
2.3. Analytical MethodsThe water displacement technique was used to measure biogas that evolved from the anaerobic digestion (AD) process [14]. COD, which is measured based on the quantity of oxidant (Cr+6) consumed and expressed in terms of its oxygen equivalence, was determined using close refluxing according to the standard method 5220D [16, 17]. Other parameters were determined as shown in Table S3.
2.4. Experimental Design and ProcedureDesign Expert software (10.0.3) was used to perform the statistical design of experiments and data analysis. Three independent effective variables were selected: HRT, pH and OLR. The OLR is a measure of the capability of the microorganism in the AD process to breakdown organic compounds present in the effluent.
2.4.1. CCDThe CCD is a RSM design type which estimates the second order polynomial on a wider range of the design space and processes the input data to give out the interactions between the response and the process variables. The CCD is a five-level fractional factorial design, which comprises of a two level factorial design, central designs and two axial designs. The centre point is replicated to enhance the measurement of reproductively and the model lack of fit. It also has rotatability and orthogonality properties, which helps in the curvature description when represented in 3D plots. There were 30 experimental runs derived from the design matrix, with two centre points and an alpha value of 1.89. The total number of the experiments (N) depended on the replication number of the centre points. The range and levels of the variables in coded and actual units are given in Table 1.
2.4.2. BBDThe BBD is a spherical, rotatable, or nearly rotatable second-order design. It is based on a three-level incomplete factorial design, which consists of the centre point and middle points like the edge of a cube. Although, BBD can be derived from a cube, it can be represented spherically, making the vertices of the cube not covered by the design. It can be considered as three interlocking factorial designs along with centre points. The BBD is said to be a more economical and viable tool than the CCD, because its design matrix are usually generated with a fewer number of experimental runs [3, 6].
As shown in Table 1, three levels were chosen for the independent variables (operating variables). The CCD and BBD experimental design were conducted for the three factors and the two responses (COD removal and biogas production). Other parameters that were monitored alongside were the alkalinity, Volatile Fatty Acids (VFA), Total Suspended Solids (TSS) and Volatile Suspended Solids (VSS). The parameters were chosen to indicate the performance of the reactors in terms of operational stability and efficiency.
Where xn, xo and Δxn represent the coded level, the real value, the centre point value and the variable step change, respectively.
A second order polynomial Eq. (3) was used to describe the effect of the chosen parameters and their interactions on the responses using the BBD for the experimental design.
Where βo, βi, βii and βij are constant, linear, quadratic, and cross factor interaction coefficients, respectively; Xi and Xj represent the independent variables; Yi is the predicted response; and k and c are the number of factors and the residual terms, respectively. The significance of the model equations, individual parameters and factor interaction were evaluated by the analysis of variance (ANOVA) at a confidence intervals (CI) of 95% (ρ = 0.05). Two-dimensional (2D) contour plots and three-dimensional (3D) surface responses were obtained after applying the developed quadratic models.
3. Results and DiscussionTreatment efficiency for the UASB was observed to be above 65% of the contaminants removal. VFA, alkalinity, TSS and VSS, respectively were reduced to 64.9 ± 2.5, 92 ± 5.5, 35 ± 7.8 and 125 ± 8.6 mg/L. A significant desludging of 5 ± 1.5 mg TSS/L was carried out to reduce the UASB sludge volume intermittently. RSM was employed to reduce the number of experiments by selecting a small number of experiments, which were best representatives of the test domain to investigate the responses (COD and biogas).
Tables S4 and S5 illustrate the experimental matrices, which have 16 factorial points, 8 axial points and 6 centres points. They were then evaluated using multiple regression analysis of the CCD and BBD adapted from the RSM. The ANOVA was employed to evaluate the significant effect of the regression models statistically. The regression models mathematically explained the relationship between the responses and the independent variables on the system. The visual representation of the responses is graphically presented in 3D surface and 2D contour plots. The regression models developed using CCD and BBD together with the experimental data are expressed in coded and actual values as depicted equations 4–7 for CCD and 8–11 for BBD. The combination of the factors at different levels showed effective responses of the models, with the models predicted value and experimental value difference being less than 5%. The experimental data were well fitted to the quadratic polynomial function.
From the equations for both the CCD (Eq. (4)-(7)) and BBD (Eq. (8)-(11)), the models developed showed a good fit to the quadratic design space with high regression coefficients. Quadratic models had high R2 (0.9606; 0.9782), adjusted R2 (0.9429; 0.9614) and predicted R2 (0.8499; 0.8945) values for the CCD and BBD, respectively. All the models were significant with an insignificant lack of fit (LOF) at the 95% confidence level. The BBD based models had superlative values for the R2 as compared with the CCD. The response models developed and their respective predicted values were then evaluated to validate the experimental results for the treatment of the wastewater using UASB. In addition, the models derived by the BBD seem to be simpler than the CCD, which had only 9 terms, whereas the CCD had 10. According to Zolgharnein et al. [6], the simplicity of the BBD makes it stand out from a theoretical statistical standpoint for better prediction. The response models, due to their complexity, validity, accuracy and operational interactions were then compared (section 3.1) with respect to their design’s performance.
3.1. The Analysis of Variance (ANOVA) and Significance of the Models Using CCD and BBDThe ANOVA is essential in determining the significance and adequacy of the model. From model equations for both the CCD and BBD, the models developed were expressed in terms of their coded and actual values. The relationship and interactions between the HRT (A), OLR (B) and pH(C) and the responses were established by applying the multiple regression analysis. With the ANOVA, the statistical values of the model terms were determined. Tables 2 and 3 depict the ANOVA summary of the CCD and BBD for the COD based models, respectively. Likewise Tables 4 and 5 show the biogas production using CCD and BBD. In terms of the CCD, the coefficient of determination (R2) for COD and biogas were 0.9617 and 0.9653, respectively. In addition, the R2 of the COD and biogas-based models using the BBD were 0.9752 and 0.9802, respectively. In both occurrences the R2 values were found to be greater than 0.8 indicating a good fit of the models. Each of the model terms evaluated by the F-test showed 5% significance level (p < 0.05) with a p-value (probability) of 95% confidence level. The CCD and BBD F-values for COD (47.70; 3.37) and biogas (3.31; 9.02) implied that there was less than 2% chance that an F-value that large could occur due to error. Hence, the significant terms with p-values less than 0.05 were considered as significant terms, whilst those with p ≥ 0.05 were considered as limited terms. The high hierarchal were of the model terms with p-values greater than or equal to 0.05, which had limited influence on the response were also excluded. The adequate precision measured the signal to noise ratio.
The adequate precision ratio and the low values of the coefficient of variation (CV) validated the reliability and good precision of the models as shown in Table 2–5. A precision greater 4 indicated that the model was significant while the CV should be ≥ 0.1. The ANOVA results prove that the response surface models for predicting the COD and biogas yield are considerably coherent. This is due to the high R2 values, which satisfied the adjustment of the models to suit the experimental data. This demonstrated a good agreement between the experimental data and the predicted results (Table S4 and S5). Furthermore, the ANOVA results showed a desirable and coherent agreement with the adjusted R2. Therefore, the use of the quadratic models could be used to optimize the system under the same given condition instead of the conventional method.
3.2. Diagnostic Checking of the Fitted Models Using CCD and BBDTo authenticate the normality assumptions, the normal probability plot of residuals was used. Such that, if the residuals plot approaches a straight line, then the normality assumption is satisfied. According to Zolgharnein et al. [6], although some points are anticipated to scatter evenly, if the data points falls along the straight line then it is acceptably significant. Fig. S3 and S4 show that the normal probability vs the studentized residuals plots for both CCD and BBD, respectively. The plots for the CCD and BBD responses suggest that the random scattering of the point is distributed along the line. However, some of the points were evenly distributed, hence indicating a constant variance of the response. Fig. S4 and S5 presented the predicted vs experimental value plots, which demonstrated that the predicted values depended on the main effect of the factor levels. Hence, it is important to identify these influential factors and their levels to ascertain the significance of the model. As depicted in Fig. S5 (a) and (b), the removal efficiency of the COD ranged from 72% to 88% and for biogas production from 4,200 mL/d to 5,700 mL/d, respectively for the CCD. In Fig. S6(a) and (b), COD removal of 78% to 88% and biogas production of 3,800 mL/d to 5,800 mL/d was obtained by using the BBD.
3.3. The Three-dimensional (3D surface) Plots of the ModelsTo graphically analyse the interactive relationships among the factors and the response, the Design Expert 10.0.3 generated the 3D surface. The visual representation of the response surface in 3D surface plots assisted the investigation and optimization of the UASB, by determining the maximum region of interest on the curvature of the surface. The precise location and optimum point identified (Fig. 1 and 2) indicated the true representation of the regression Eq. (4)-(11). The 3D surface showed the model’s variation with two factor levels (HRT and OLR) whereas the other factor level (pH) was kept constant. In addition, the plots depict the sensitivity of the responses due to the change of factor levels with the degree of their interactions. Fig. 1(a) and 1(b) illustrated the maximum COD removal (72–88%) and biogas produced (3,500–5,500 mL/d) at a pH of 7 using CCD. While, Fig. 2(a) and 2(b) also depicts response surface plots at a pH of 7 for maximum COD removal (77–90%) and biogas production (3,714–5,600 mL/d) using BBD. All the 3D surface plots depict the effect of HRT and OLR on COD removal and biogas production at alkaline medium. The optimization of the process variables was aimed at finding the levels of the factors to obtain a maximum desirability for all the responses within the design space.
3.4. Numerical Evaluation of the Effect of pH, OLR and HRT on the Response
Table S1 and Fig. 3 shows some of the CCD suggested optimal conditions using the numerical analysis. Likewise, Table S2 and Fig. 6 do the same for the BBD response model. Comparatively, high desirability performance of the BBD (94%) was obtained as compared to the use of the CCD at 92%. However, almost the same optimum conditions such as HRT (15 h) and pH (7) were obtained by using the CCD and BBD, except the OLR that differed as 3.5 kg.m−3.d−1 and 3 kg.m−3.d−1, respectively.
A series of mechanism occurred in the reactor to enhance the microbial community in breaking down the organic matter. These mechanisms enhanced the biodegradability to generate more biogas during the digestion process, which includes the acidogenesis and methanogenesis that occurred at different pH levels. The control of the pH was very critical to detect the abnormalities in the system in respect of acidity and alkalinity, which might inhibit the system. From the results, it was found that high OLR (10 kg.m−3.d−1) at low HRT (8 h) could result in high VFA, which might have inhibited the biogas production and decrease the degradability of the COD. Thus, within the pH range of 6.5–7.2, the COD removal and biogas production increased, whilst below 6.5, the efficiency of the system was inhibited. This agree with the report by Lettinga and Pol [15 Lettinga and Pol [15] and Torkian et al. [18 Torkian et al. [18]. They reported that a decrease in pH below 6.5 could hinder the methanogenic microorganism activities thus declining biogas production. At a lower pH, an accumulation of VFA could occur and a minimal buffering capacity of the UASB is induced thereby inhibiting the methanogenic activity.
The OLR rate describes the liquid flowrate and contaminant concentration and can be defined as the mass of the pollutant introduced in a unit volume of the reactor per unit time. As such, this parameter integrates reactor characteristics, operational characteristics, and bacterial mass and activity into the volume of media Ruiz et al. [19]. plays a significant role on the performance of the UASB reactor. With an increase in the OLR, an increase in the biogas production was experienced. However, at an OLR above 5 kg.m−3.d−1 and at a shorter HRT of less than 8 h was found to be detrimental to the methanogens. Thus, the high OLR (10 kg.m−3.d−1) resulted in poor performance of the system, due to overload of the substrate, which supersedes the microorganism. At a lower HRT, there is a reduction in the contact time for the breaking down of the organic components, therefore impeding the performance of methanogens present in the system such that the conversion of the high COD or the acetates into biogas is limited. Operating at an optimal region of the OLR (3–5 kg.m−3.d−1) was found suitable to prevent the washout of the organic matter in the effluent and increased the treatable desirability of the system. At higher OLR, a possible washout of organic matter could occur.
The HRT is considered an important operating paramter, such that its effectiveness is the controlling factor with respect to the entire UASB performance. The observation of a long HRT (18 h) could lead to a siutuation in the reactor whereby the microorganism would compete over the available the substrate in other to withstand adjust to the discomfort. This phenomenon can affect the growth rate of the microbial community in the reactor, even though a higher yield of biogas and degradability could be achieved as seen with a HRT of 8–15 h.
A confirmation test (Fig. 3) was carried out with the selected optimum conditions in Tables S1 and S2 with highest desirability through the numerical optimization analysis ramp plots (Fig. S1 and S2) provided in the supplementary section. It was found that the BBD based model predicted values agree with the experimental results with less than 2% disparities. Whereas, the CCD based model predictions was greater in terms of COD removal (82.6 ± 1.06% > 80.8%) and biogas production (4,636.31 mL/d ± 439.81 < 5,800 mL/d) which was less than the experimental results. This made the BBD to be more superior over the CCD.
4. ConclusionsOptimization of multiple variables is a major concern in wastewater treatment processes to the obtainability of the desirable discharge effluent limits. This research paper was aimed at comparing the applicability of CCD and BBD for the optimization of HRT, pH and OLR in determining their desirability efficiency in a UASB for the treatment of wastewaters. The two response surface designs investigated produced almost the same optimum conditions: HRT (15 h) and pH (7), except the OLR that differed as 3.5 kg.m−3.d−1 and 3 kg.m−3.d−1 for CCD and BBD, respectively. Both designs were found suitable in predicting high treatability performance of the UASB above 90%. Based on the confirmation test, the BBD model prediction (biogas 5,955.4 ± 225.3 mL/d; COD 81.5 ± 1.014%) was found to be in good agreement with the experimental results (biogas 5,800 mL/d; COD 80.8%). Conversely, the BBD produced a high desirability efficiency of 94% as opposed to the CCD of 92%. The models obtained were found to be predictive, adequate and significant at 95% confidence level. RSM is an effective and economically viable alternative technique that can be adapted for optimizing various wastewater treatment processes to favourably maximise the output. Operating the UASB at HRT (8 to 15 h), OLR (3 to 5 kg.m−3.d−1) and pH (6.5 to 7.2) were found to be workable conditions to maximise the outputs. Furthermore, the UASB is an effective and reliable process for the treatment and generation of biogas from wastewaters. In addition, this area can be of economic interest to stakeholders for protecting the environment and producing green energy as well as reducing the footprint of greenhouse gases.
AcknowledgmentsThe authors wish to thank Durban University and South Africa National Research Foundation (NRF) for their support.
References1. Tetteh EK, Rathilal S, Chollom MN. Treatment of industrial mineral oil wastewater-optimisation of coagulation flotation process using response surface methodology (RSM). Int J Appl Eng Res. 2017;12:13084–13091.
2. Dasgupta J, Sikder J, Chakraborty S, Curcio S, Drioli E. Remediation of textile effluents by membrane based treatment techniques: A state of the art review. J Environ Manage. 2015;147:55–72.
3. Bezerra MA, Santelli RE, Oliveira EP, Villar LS, Escaleira LA. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta. 2008;76:965–977.
4. Ibrahim S, Wahab NA, Anuar AN, Bob M. Parameter optimisation of aerobic granular sludge at high temperature using response surface methodology. Int J Electr Comput Eng. 2017;7:1522–1529.
5. Najib T, Solgi M, Farazmand A, Heydarian SM, Nasernejad B. Optimization of sulfate removal by sulfate reducing bacteria using response surface methodology and heavy metal removal in a sulfidogenic UASB reactor. J Environ Chem Eng. 2017;5:3256–3265.
6. Zolgharnein J, Shahmoradi A, Ghasemi JB. Comparative study of Box-Behnken, central composite, and Doehlert matrix for multivariate optimization of Pb(II) adsorption onto Robinia tree leaves. J Chemometr. 2013;27:12–20.
7. Bashir MJ, Amr SSA, Aziz SQ, Aun NC, Sethupathi S. Wastewater treatment processes optimization using response surface methodology (RSM) compared with conventional methods: Review and comparative study. Middle-East J Sci Res. 2015;3:244–252.
8. Bashir MJ, Aziz HA, Aziz SQ, Amr SA. An overview of wastewater treatment processes optimization using response surface methodology (RSM). In : The 4th International Engineering Conference–Towards engineering of 21st century; 15–16 January 2012; Gaza.
9. Pambi R, Musonge P. Application of response surface methodology (RSM) in the treatment of final effluent from the sugar industry using Chitosan. In : WIT Transactions on Ecology and the Environment; 27–29 June 2016; Venice. p. 209–219.
10. Amr SSA, Aziz HA, Bashir MJ. Application of response surface methodology (RSM) for optimization of semi-aerobic landfill leachate treatment using ozone. Appl Water Sci. 2014;4:231–239.
11. Chong S, Sen TK, Kayaalp A, Ang HM. The performance enhancements of upflow anaerobic sludge blanket (UASB) reactors for domestic sludge treatment – A state-of-the-art review. Water Res. 2012;46:3434–3470.
12. Bustillo-Lecompte CF, Mehrvar M. Treatment of an actual slaughterhouse wastewater by integration of biological and advanced oxidation processes: Modeling, optimization, and cost-effectiveness analysis. J Environ Manage. 2016;182:651–666.
13. Phanduang O, Lunprom S, Salakkam A, Reungsang A. Anaerobic solid-state fermentation of bio-hydrogen from microalgal Chlorella sp. biomass. Int J Hydrog Energ. 2017;42:9650–9659.
14. Jha P, Kana EBG, Schmidt S. Can artificial neural network and response surface methodology reliably predict hydrogen production and COD removal in an UASB bioreactor? Int J Hydrog Energ. 2017;42:18875–18883.
15. Lettinga G, Pol LH. UASB-process design for various types of wastewaters. Water Sci Technol. 1991;4:87–107.
16. Rezaee S, Zinatizadeh AA, Asadi A. High rate CNP removal from a milk processing wastewater in a single ultrasound augmented up-flow anaerobic/aerobic/anoxic bioreactor. Ultrason Sonochem. 2015;23:289–301.
17. Chollom M, Rathilal S, Swalaha F, Bakare B, Tetteh E. Study of the start-up of an upflow laboratory-scale anaerobic sludge blanket for the treatment of slaughterhouse wastewater. In : 4th Water and Society internatioanl conference; 4–6 June 2017; Seville, Spain.
Fig. 1CCD -response surface plot effects of HRT and OLR at constant pH (7) on (a) COD removal (b) biogas production on 3D surface plot. 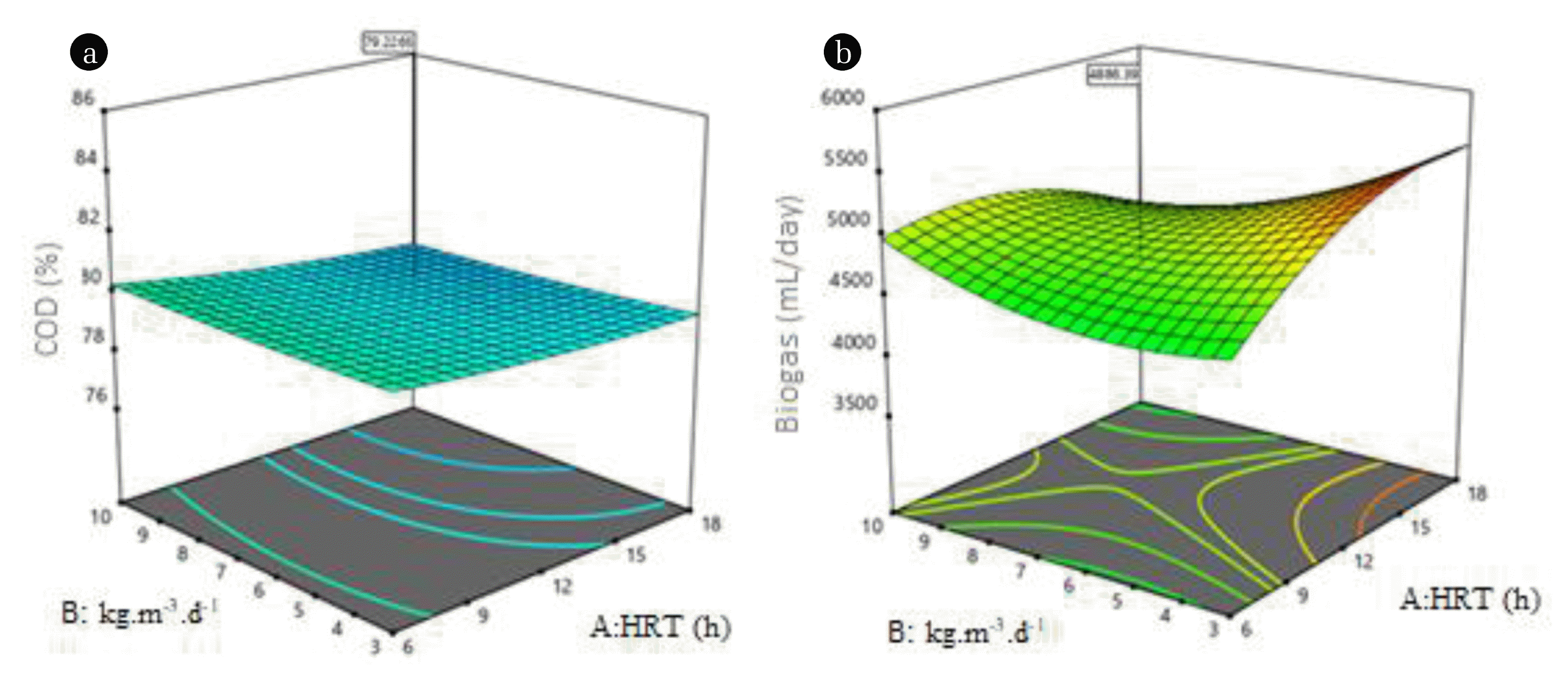
Fig. 2BBD -response surface plot effects of HRT and OLR at constant pH (7) on (a) COD removal (b) on biogas production on 3D surface plot. 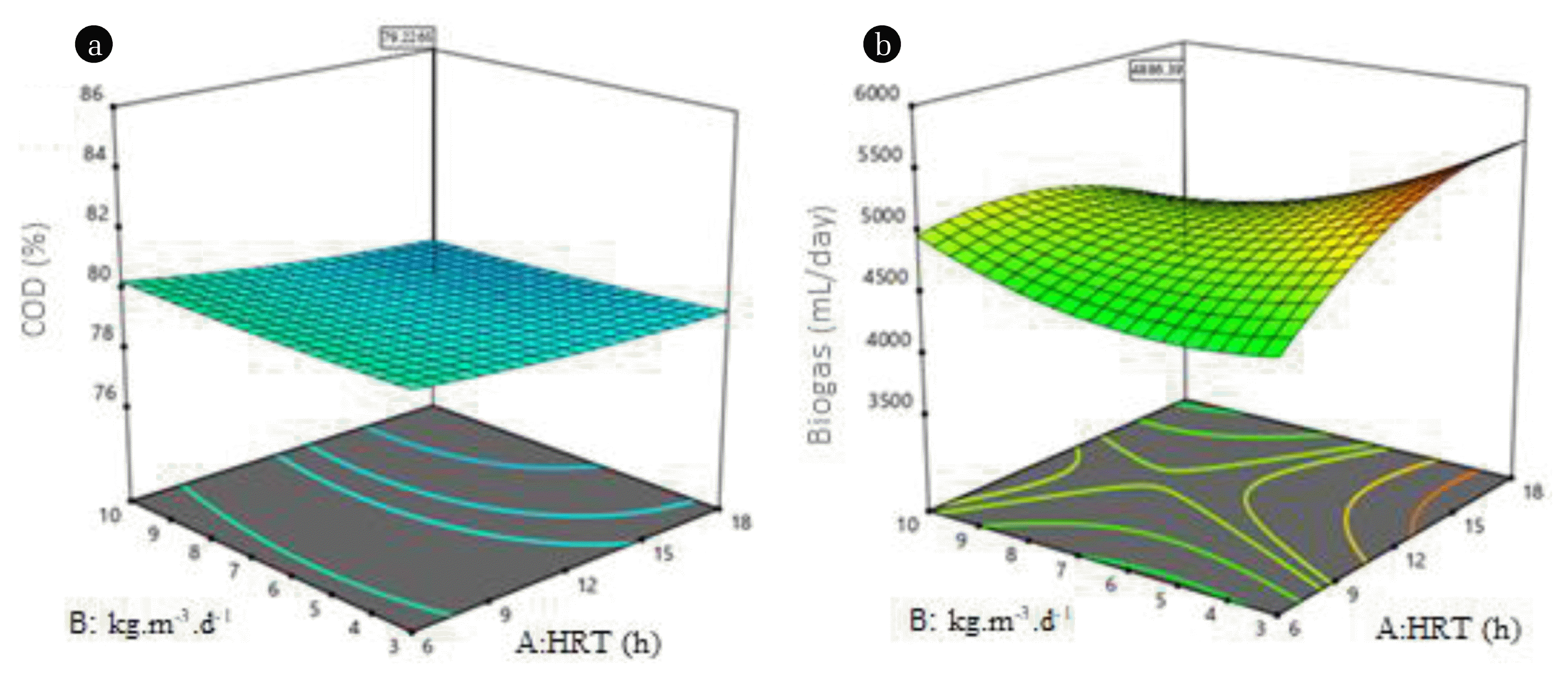
Table 1Experimental Design Inputs and Factors
Table 2ANOVA Results and Adequacy of the Quadratic Models for COD Using CCD Table 3ANOVA Results and Adequacy of the Quadratic Models for COD Using BBD Table 4ANOVA Results and Adequacy of the Quadratic Models for Biogas Using CCD Table 5ANOVA Results and Adequacy of the Quadratic Models for Biogas Using BBD |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||