BFA, used as an adsorbent in the present study, was obtained from a nearby sugar mill. It was used as such without any kind of pre-treatment. Exhaustive physico-chemical traits of the BFA are already presented the literature [11–13]. The average particle size of BFA was 167.35 μm. Proximate analysis manifested the presence of 7.6% moisture, 17.4% volatile matter, 26.4% ash and 49.6% fixed carbon in BFA. Bulk density of BFA was determined as 133.3 kg/m³. The d-spacing values provided by the XRD spectra of BFA reflected the presence of alumina (Al₂O₃), silica (SiO₂), CaO, CaSiO₃, and Ca₈Si₅O₁₈. The pore surface area of BFA was found to be 171 m²/g, whereas BJH adsorption/desorption surface area of pores was 54.2/49.9 m²/g. The average pore diameter of BFA was found to be 23.9 Å whereas the BJH adsorption/desorption average pore diameter was 39.4 Å/33.9 Å.

The concentration of furfural was determined by using UV-spectrophotometer (HACH, DR/5,000). Maximum absorbance for this was obtained at a wavelength (λ_max) of 277 nm and the same was used to plot a model graph to relate absorbance and furfural concentration in the solution. The graph showed linear limit up to maximum furfural concentration of 10 mg/L. Therefore, for reliable determination of the furfural in samples, dilution was done using distilled/milliQ water, for the samples having a concentration higher than 10 mg/L of furfural so as to lower the concentration of furfural below 10 mg/L [1].

Schematic representation of experimental set up is given in Fig. 1. A thermostatic heating device was used in the chamber in which the column assembly was kept so as to control the temperature and maintained at 303 ± 1 K. A plexiglas column having inside diameter (D) of 2.54 cm and length 90 cm was used for the experimental studies. The feed port for the column was provided at the bottom center of the column. Glass beads of 0.2–0.3 cm diameter were used to fill the lower portion of the column up to a height of 1.5 cm. This was done to distribute the solution uniformly across the whole cross section of the column. Varying heights (Z = 15, 30, 45 and 60 cm) were chosen from the bottom to pack BFA in the column. Aqueous solution of furfural was pumped (upward flow) to bed using a peristaltic pump (Miclins PP20). The C_o and Q were varied in the range of 50–200 mg/L and 0.02–0.04 L/min, respectively. pH of the furfural solution in all experiments was 5.5.

To achieve 100% wettability of packing inside the bed, an upward flow was adopted in the study presented. If done otherwise, it necessitated the use of specifically modelled distributors of liquid such that complete distribution of liquid is achieved inside bed [14]. Often, the holdup decreases as the liquid flow rate falls and the disturbance it causes in distribution of liquid poses great threat to the process efficacy [15, 16].

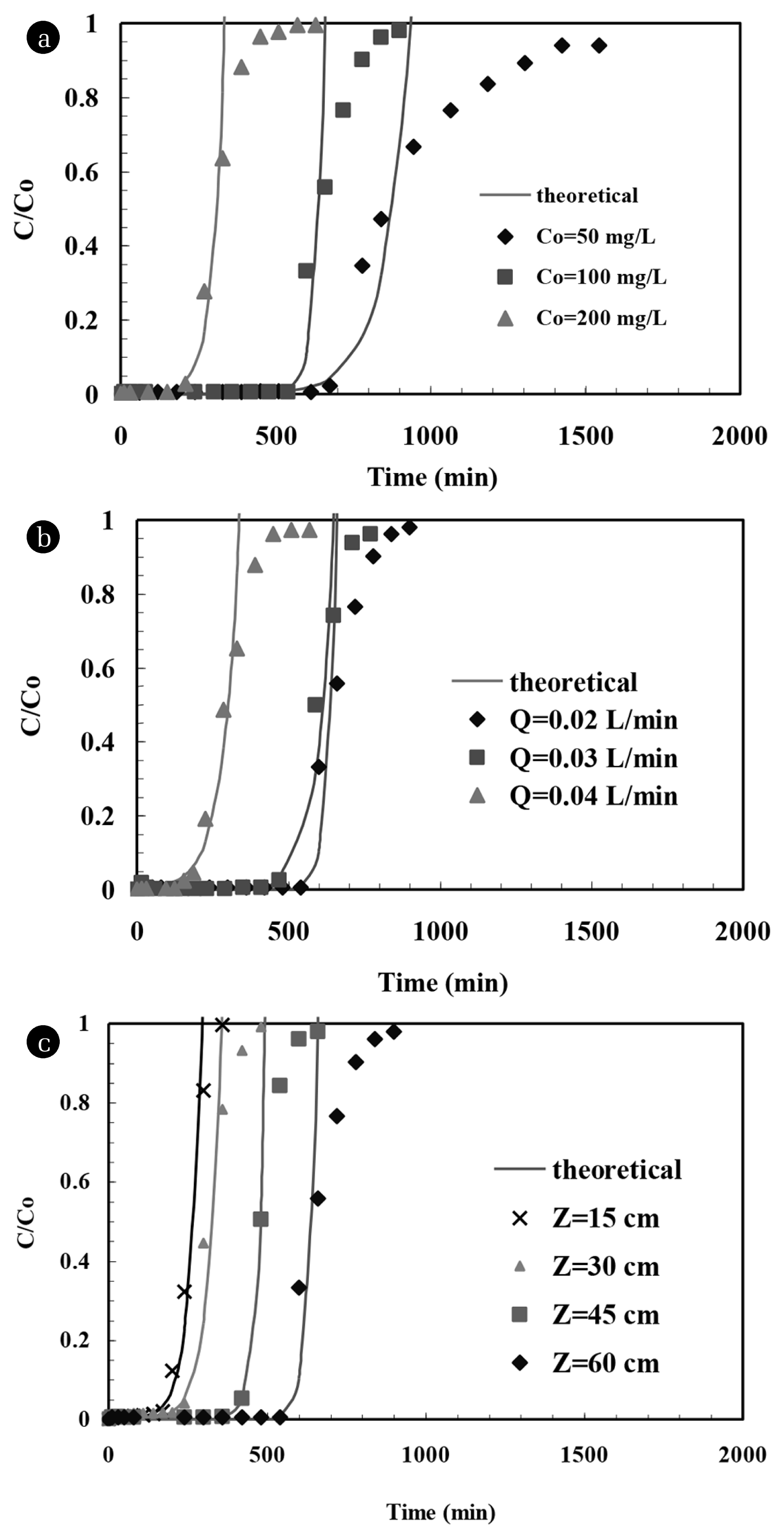
A typical experimental breakthrough curve is shown in Fig. 2(a). It was found that the furfural adsorbed on BFA was initially rapid such that the bulk solution released from the bed was having zero furfural in it. But the BFA started to satiate gradually as the furfural containing feed is fed for further time, and as a result, the amount of furfural in the bulk solution at outlet started to increase until the bed fully gets satiated. During actual operation, process is suspended as the amount of furfural in outlet solution increases up to a specified limit, known as breakthrough concentration, after which it is not suggested to proceed with the process. In the present study, the operation is continued till the bed reaches its satiation point. During estimation of typical variables of the system, breakthrough amount of furfural C_BP (10% of C_o) was set, and the time corresponding to this concentration was considered as breakthrough time (t_BP).

The idea of the mass transfer zone (MTZ) was initially introduced in fixed bed columns’ operation to understand the evolution patterns of the various parameters and to plan an efficient model for better performance during sorption in a fixed bed column [17, 18]. Significant sorption at any adsorbate inside the bed occurs in this MTZ [19]. Fractional capacity (F), the height of MTZ (H_Z) and the speed of the MTZ along the bed height (U_Z) determine the characteristics of the MTZ. They help us understand the way the adsorption process inside the bed advances. Various parameters of system can be expressed directly or indirectly using these parameters that control the overall sorption inside the bed. F is the term obtained when the proportional amount of adsorbent actually involved in sorption is divided by the total amount of adsorbent utilized for MTZ. In other words, it can be stated as the ratio of actual amount of adsorbate removed from the solution to the ideal extent of adsorbate removal by the adsorbent within the MTZ [17–19]. F is given as:

where, V_E is the bulk amount of effluent treated at the point of exhaustion time (t_E) with immediate concentration (C_E) equivalent to 90% of the amount in effluent (C_o) at the start of process. Based on the fashion in which the bed is operating, this amount in effluent in selected randomly while keeping the process as economized as possible. V_BP is the bulk amount of effluent treated at point of breakthrough time (t_BP) with immediate concentration (C_BP) which is lower than 10% of the amount present at the start of the process.

H_Z is the area where practically all sorption takes place. It plays a significant role in evaluating the removal rate of adsorbate by the BFA, and guides regarding the diffusion resistances present during the process. The lower the resistance offered by the system, more the kinetics of uptake of adsorbate paces and shorter is the height of MTZ at any given instant. Thus, it proves to be a significant variable in figuratively estimating the overall kinetics of the uptake during the process. H_Z is formulated as:

U_Z is basically used to evaluate the behavior of sorption in a fixed bed with continuous flow when a state of equilibrium is reached. It is basically an output function corresponding to the adsorbent’s uptake potential, and thus, allows estimating the bed saturation rate. Being directly proportional to H_Z, it shows that as the H_Z decreases, uptake rate of adsorbate increases, and the fixed bed satiates at a much faster rate [17–19]. U_Z is given as:

In order to find the efficacy of overall bed, we need to find number of unit transfer equivalents (N_Z) [17]. It is given as:

For a rapid uptake of adsorbate by adsorbent, lesser is H_Z and higher is N_Z. Other than this, during a dynamic uptake process, larger values of N_Z is avoided in order to avoid the rapid satiation of bed.

The influence of C_o on breakthrough curves is shown by data points in Fig. 2(a) and the results are tabulated in Table 1. It is evident from the figure that t_0.1 decreased with an increase in the C_o. At lower C_o, curves were sparser and breakthrough occurred sluggishly. As the value of C_o increased, the slope of breakthrough increased [20]. These results establish that any alteration in concentration gradient also alters the bed usage rate and the breakthrough time [21]. This occurs because large number of sorption sites gets occupied with an increase in C_o. As the value of C_o increases, mass transfer driving force is seen to over-power the resistance offered by solution [22, 23]. This phenomenon helps the bed to increase its fractional capacity (F). Also, along with the increase in furfural loading rate, which further causes the shortening of the sorption zone length (H_Z) due to the increase in kinetics of process [17, 24]. As N_Z varies inversely to H_Z, a rise in its value is seen on the onset of increase in C_o. Also, due to rapid satiation of sorption sites, U_Z is seen to increase progressively with the increase in C_o [18, 25].

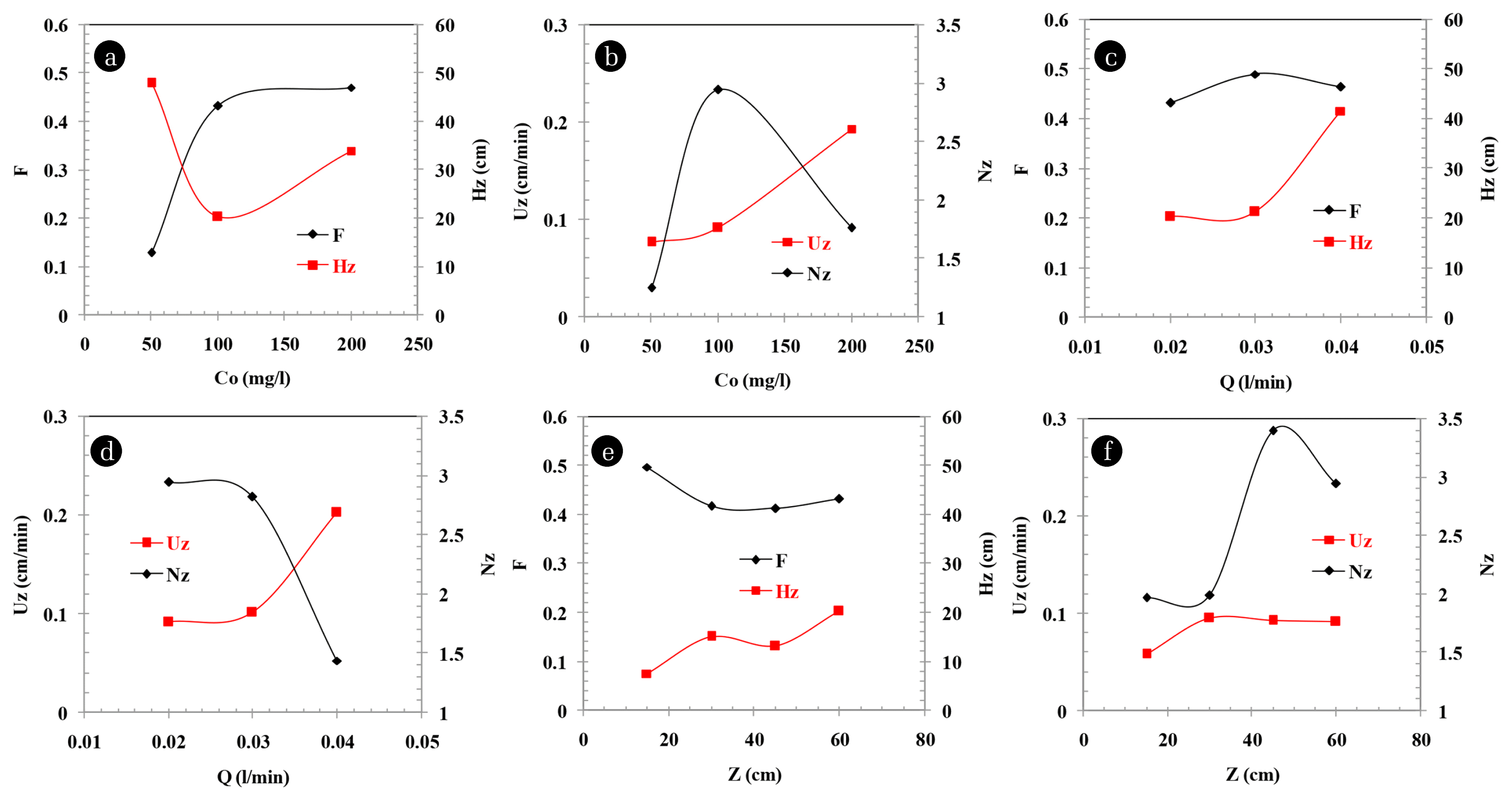
The effect of C_o on F, H_Z, U_Z and N_Z is shown in Fig. 3(a) and (b). The value of F (as per expectation) can be seen increasing from the graph as C_o increases, until a maximum capacity limit of 0.435 for C_o (= 100 mg/L) is achieved. After this, C_o doesn’t affect much on F as the bed has already reached its maximum fractional capacity due to increase in C_o keeping every other parameters constant. In accordance to the increasing F, H_Z can be seen decreasing to the point when C_o reaches 100 mg/L making H_Z minimum at 20 cm. Further this point, H_Z again starts to increase as the bed reaches its limit of sorption capacity for the MTZ at any given instant. N_Z rises to a maximum value of 3 at C_o (= 100 mg/L) and further decreases as we increase C_o. A fashion of rise and decline N_Z is due to the decrease of MTZ height during the first phase when C_o varies from 50–100 mg/L and then, increase in MTZ height after further increasing C_o, respectively [19, 26]. Also, U_Z is increasing as we move from (50–200) mg/L. U_Z is basically related directly with the satiation of column and increasing C_o ensured a rapid sorption.

The breakthrough curves obtained for three Q (= 0.02, 0.03 and 0.04 L/min) at constant Z (= 60 cm) and C_o (= 100 mg/L) were investigated. The experimental breakthrough times deduced from Fig. 2(b) are shown in Table 1. The value of t_0.1 decreased as the value of Q increased. Inclusive of this, decreasing Q also resulted in the widening of breakthrough curve, which resulted in further increase in the difference between the breakthrough time and the saturation time. As anticipated, steeper curves with short mass transfer zone are seen due to reduction in breakthrough and exhaustion times, whenever there is a rise in Q [26–28].

The effect of Q on F, H_Z, U_Z and N_Z is shown in Fig. 3(c) and (d). At lower Q (0.02 and 0.03 L/min), resistance for transfer of furfural from solution to adsorbent is less, thus, the removal of adsorbate is faster. Therefore, H_Z and U_Z are less at lower Q (0.02 and 0.03 L/min) as compared to at higher Q (0.04 L/min). At lower Q (0.02 and 0.03 L/min), shorter H_Z increases the value of N_Z, therefore, the exhaustion of bed is better (i.e., better occupation of sites). This leads to increase in F. At higher Q (0.04 L/min), very less time is available for the volume element of solution to contact with the fixed bed which is inadequate to achieve equilibrium [19, 25]. This further leads to low sorption of adsorbate from the solution being fed at high Q.

The value of F is higher at Q = 0.03 L/min as compared to that at Q = 0.02 L/min. Generally, when Q is lowered, the liquid holdup gets decreased too and liquid maldistribution thus caused may show its impact on the efficacy of the bed [16]. At smaller liquid holdup, it is possible that some amount of the adsorbent may not get properly wet with the solution, and thus, don’t participate in the sorption process and stay unutilized. Also, this improper circulation of solution may cause liquid to flow through a favorable channel in the bed and leave the rest of bed untouched [29]. The lower value of F at Q = 0.02 L/min may be attributed to channeling. As per the recent developments, it is seen that larger values of Q > 0.03 L/min are generally not preferred as it leads to rapid arrival of breakthrough and lesser sharp-edged.

The breakthrough curves for furfural sorption (shown in Fig. 2(c) by data points) were investigated at four different Z (= 15, 30, 45 and 60 cm) at a constant Q = 0.02 L/min and C_o = 100 mg/L. It can be seen that the t_BP was lower for the lower values of Z, and increased with increase in Z due to the increase of the available surface area and binding sites for the furfural sorption. The breakthrough curves got flattened with an increase in Z. This is due to the widened mass transfer zone that cause breakthrough curve to be less steep. The breakthrough curves for the lowest Z showed a very little “tail” approaching saturation time because of the lesser amount of the BFA present inside the bed. As the value of Z is increased, a steep S shape breakthrough curve was seen [26, 28]. Due to intra-particle diffusion or non-idealities in flow at higher Z, breakthrough curves showed a broad tailing edge [30]. These results clearly reflect that the bed having greater value of Z was more difficult to completely exhaust as compared to bed having low value of Z [22, 25, 31, 32].

Empty bed contact time (EBCT) can be calculated using the following equation:

The performance of an adsorbent packed bed is formulated in reference to the adsorbent usage rate (U_r). U_r is stated as the mass of adsorbent used per liter of solution treated [33].

where, V_C is the volume of the BFA in the packed-bed (L), A_C is the cross-sectional area of the packed-bed (cm²), m_C is the mass of the BFA in the packed-bed (g), V_BP the volume of treated effluent discharged till breakthrough (L), ρ is the apparent density of the BFA (g/cm³) and N_BP is the bed volumes of the effluent to breakthrough.

Choosing 10% breakthrough point as the end point, the values of EBCT and U_r were evaluated and the results are given in Table 1. As per the definitions, lower values of U_r and higher values of N_BP are desirable. Obtained results show that U_r generally increased and N_BP generally decreased with an increase in Z, C_o and Q. Adsorbent mass has a negative effect on N_BP and U_r. Higher values of U_r and lower values of N_BP were found at higher Z. In spite of more binding sites available for sorption at higher Z, not all of them were accessible to the furfural molecules. This was due to operational problems such as axial dispersion, channeling and bed compaction [34, 35]. This behavior has been reported earlier as well [36]. For C_o as variable parameter, it is obvious that higher amount of furfural at higher C_o will exhaust the bed early and U_r values would be higher which is undesirable. The amount of furfural molecules that enter the packed-bed increase the adsorption rate, causing higher values of U_r and lower values of N_BP. Similar results were found by other authors as well [36, 37]. With an increase in Q from 0.02 L/min to 0.03 L/min, positive effect (lower values of U_r and higher values of N_BP) was observed. This was because of the decrease in film which offers mass transfer resistance around BFA particles [38]. However, further increase in Q to 0.04 L/min decreased the performance (higher values of U_r and lower values of N_BP) because of the inadequate residence time of the liquid phase in the packed-bed and availability of less time for furfural diffusion into the pores of the BFA [39, 40].

During sorption operation in any packed bed, the main motive is to minimize the concentration in the effluent so that it does not go beyond critical limited of C_BP. During start, when the BFA is fresh and unsaturated, the actual effluent concentration does not exceed C_BP. As pumping of furfural solution is continued through the bed, the BFA uptake capacity starts to decrease and the effluent concentration increasingly approaches C_BP i.e., the breakthrough point is attained. Different models are utilized by researchers in the literature for the estimation of breakthrough time. In this current work, bed depth service time (BDST) and Thomas models have been utilized for the estimation of the breakthrough time for furfural sorption onto BFA. Srivastava et al. [33] have shared in the literature the theory linked to these models.

Earlier work on the BDST model was done by Bohart and Adams [41], who formulated a correlation between Z and breakthrough time (t_BP). The description of initial phase of breakthrough curve is done generally using Bohart-Adams model [42]. As for the rest of the typical operational variables of the system, they can be evaluated from the plot of C/C_o against t for a set value of Z and Q [25, 41]. Hutchins [43] linearized this model as follows:

where, C is the desired concentration of the furfural at time t (mg/L), k_B is the furfural sorption rate constant in the packed-bed (L/min mg), N_o is the adsorptive or saturation capacity of the BFA packed-bed (mg/L) and U is the linear flow velocity of the feed (cm/min). Here, the slope of the plot (N_o/C_oU) represents the adsorptive capacity of the system whereas the intercept (I) gives the value of rate constant k_B as per the following given equation [42]:

At halfway in breakthrough curve, when C_o/C = 2 and t = t_0.5, and therefore, the equation reduces as:

Thus, it infers a linear plot of time passing through the origin for t_0.5 against Z at 50% breakthrough, allowing N_o to be calculated. The dynamic behavior of the packed-bed sorption was predicted by BDST model given above and Thomas model given in subsequent paragraph. Coefficient of determination (R²) and Marquardt’s percent standard deviation (MPSD) were used to estimate the error between the experimental and calculated values of C/C_o [33]:

where, N represents the number of data points and P represents the number of parameters. The deviation between the experimental and calculated t_BP was calculated by using the following equation:

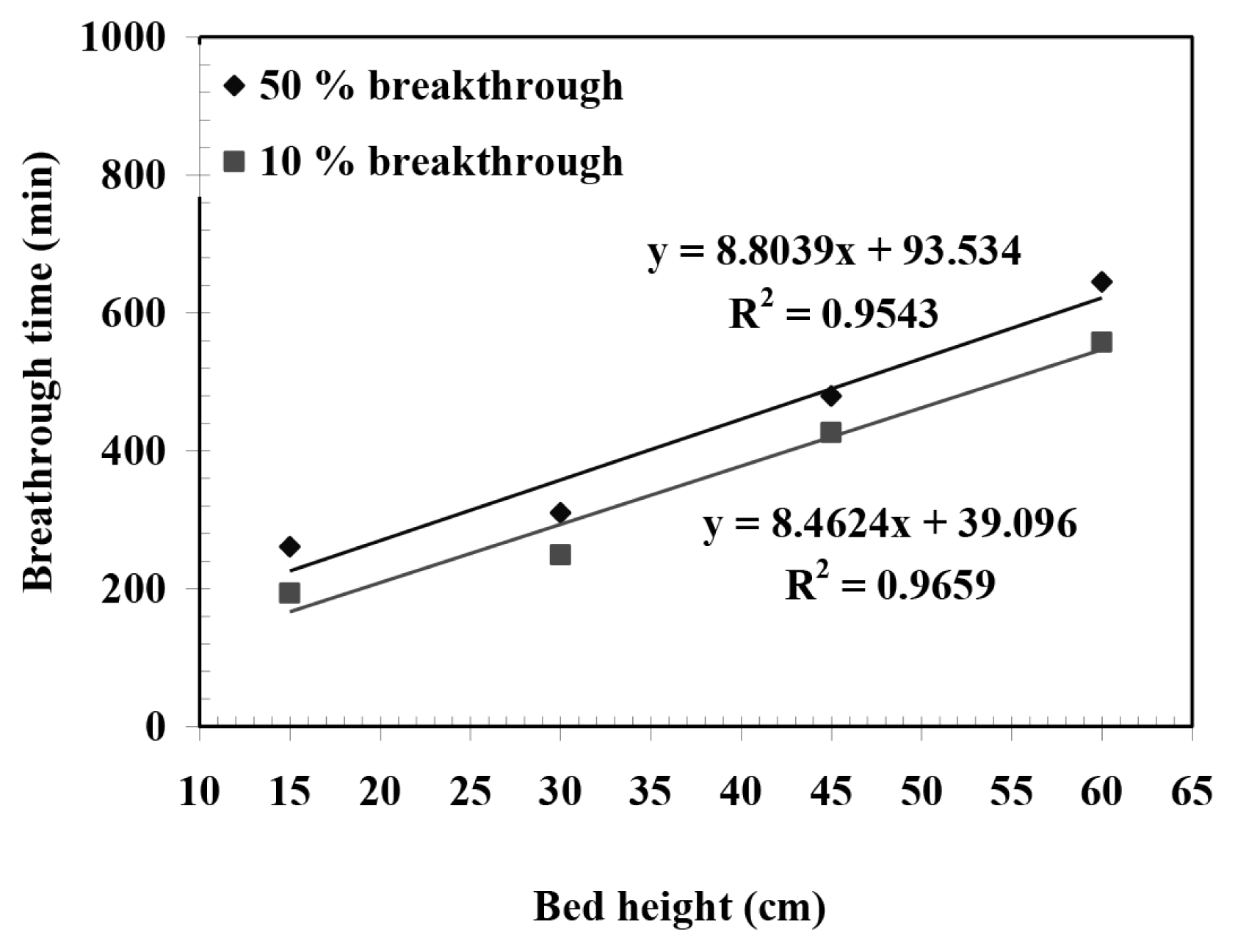
The plot of t_0.5 and t_0.1 obtained at constant Q = 0.02 L/min and C_o = 100 mg/L are against four different Z (15, 30, 45 and 60 cm) is shown in Fig. 4. It gives a linear relationship. As stated, 50% breakthrough curve between t and Z should have been a linear plot passing through the origin, however, despite being linear it does not pass through origin. This indicates that a much more complex mechanism is involved in furfural uptake using BFA and that more than one rate-limiting step exists during the process [44]. No and k as calculated from the slope and the intercept of t_0.1 versus Z plot are found to be 3,338 mg/L and 0.000562 L/mg min, respectively. N_o values showed deviation of 3.88% when compared with estimated using 10% breakthrough and 50% breakthrough plot. Fig. 2 shows the experimental and theoretical breakthrough curves predicted by BDST model at various experimental conditions. It shows a very good fit to the data up to 50% sorption of furfural. This suggests that the BDST model is valid for the relative concentration region up to 0.5. The values of N_o and k_B as calculated from Eq. (7) are tabulated in Table 2. It is seen that the value of k_B generally increases with an increase in Z and decrease in Q.

Thomas model [45] is based on the second order reaction kinetics. The linear form of the Thomas model is given as [18, 25, 46]:

where, k_T is the Thomas rate constant (L/min mg), q_o the maximum sorption capacity of the BFAe (mg/g), m_C is the mass of the BFA in the column (g), and V_eff is the throughput volume (L) [47]. The k_T and q_o can be determined from the intercept and the slope of the plot of ln[(C_o/C)−1] against t at a given Q. Thomas model was applied to the data at C/C_o ratios higher than 0.08 and lower than 0.99 with respect to Z, C_o and Q [48–50]. k_T and q_o values are shown in Table 3. Values of R² were found to be > 0.9063. Sahu et al. [1] found that the sorption kinetics of furfural onto BFA was represented by second order kinetics. Therefore, Thomas model was expected to well-represent the breakthrough curves [26]. Fig. 5 shows the experimental and theoretical breakthrough curves obtained at different Z, C_o and Q for the Thomas model. Fig. 5 and the data in Table 3 indicate that the t_0.1 values as estimated using the Thomas model were very similar to those obtained from experimental results.

Comparison of the kinetic rate constants, k_B and k_T (L/mg min), obtained by modeling the experimental breakthrough curves with the Bohart-Adams and Thomas models shows some difference in values among them, however, they were of the same order of magnitude in general. N_o in Bohart-Adams model represents saturation capacity of the adsorbent bed whereas q_o in the Thomas model represents the maximum adsorption capacity of the BFA. Values of N_o and q_o generally decreased with an increase in Z. This is because of inaccessibility of all active sites despite the increase in active sites at higher Z value which can be attributed to problems such as axial dispersion, channeling and bed compaction [34, 35]. An increase in the value of N_o and q_o was observed with an increase in C_o and Q up to certain limit. Higher load of furfural in the BFA bed at higher C_o and Q increased the driving force which increased the N_o and q_o [51, 52]. Also, the reduction mass transfer resistance because of the decrease in the size of laminar boundary layer/film around BFA particles at higher C_o and Q increased the N_o and q_o values [38]. The obtained breakthrough curves for furfural removal by BFA fitted better by Bohart-Adams model. This illustrates that the furfural and the functional groups on the surface of BFA interacted via hydrogen bonding, dipole-dipole and hydrophobic interactions among furfural and these interaction played significant role in the adsorption process [53]. Since, Thomas model is not able to better-predict the breakthrough curves than Adams-Bohart model. Hence, the external and internal diffusions seem to be the limiting steps during the sorption process [52].