1. Introduction
Wastewater, both domestic waste and industrial wastewater are still a serious problem. The process of wastewater treatment in urban areas are becoming an indispensable requirement. Treatment processes commonly used in Indonesia is the pool system or better known as waste stabilization ponds.
Waste stabilization ponds is a biological processes with organic matter in the sludges which was generated from the primary deposition and biological treatment of wastewater stably. This stability depends on anaerobic and aerobic conditions [1]. Waste stabilization ponds is used to improve quality of wastewater by relying on natural processes that treat wastewater by utilizing the presence of bacteria, algae, and zooplankton to reduce organic pollutants contained in the wastewater [2, 3].
In waste stabilization ponds, wind energy and gravity provide the movement of wastewater that led to the mass transport process. The context of the movement in the waste stabilization pond system can be divided into two general mechanisms, namely advection and diffusion. Advection refers to transport due to the bulk movement of the water which contains the solute. While diffusion is the non-advective transport due to the migration of a solute in response to a concentration gradient [4]. With the pollutant gradient horizontally and vertically in columns pond, the phenomenon of solute transport by advection and diffusion mechanisms can be described in 2-dimension (2-D) models. Mathematical model of 2-D advection-diffusion was represented by using partial differential equations based on the phenomenon of physics, chemistry and biology.
Various studies have been conducted on waste stabilization ponds, such as Sunarsih et al. [5] have present a mathematical model in the domestic waste stabilization ponds facultative with the steady state. Mayo and Abbas [6] have developed a mathematical model reduction of nitrogen compounds in waste stabilization ponds. Then, Gao et al. [7] have built a numerical model to predict the flow and transport of faecal bacteria in the water.
Research on the advection-diffusion equation which solved numerically using various methods have been carried out. In 2007, Thongmoon et al. [8] have completed the advection-dispersion equation by using finite difference method Forward Time Central Space (FTCS). Then, Rubio et al. [9] have solved transport equations for bimolecular reactive process advection-diffusion by using the finite difference method FTCS on different time scales. In 2011, Prieto et al. [10] have solved the advection-diffusion equations using finite difference methods generalized (GFDM). While Sousa [11, 12] has completed the advection-diffusion equation by using Lax Wendroff numerical methods for time discretization and then in different year, it have did by using finite difference methods of higher order.
There was also research on a comparison of several methods. Thongmoon and McKibbin [13] have completed the advection-diffusion equation of one dimension by using cubic spline, FTCS and Crank-Nicolson. Similarly, Najafi and Hajinezhad [14] have completed the same equations with the finite difference method FTCS, Upstream, Dufort Frankel and Crank Nicolson. Furthermore, Appadu et al. [15] have conducted a study to solve advection diffusion equation using 3 different numerical methods, namely third-order scheme Upwind, Upwind fourth-order and finite difference schemes non-standard (NSFD).
Dependence natural processes in pond to degrade wastewater causing the system vulnerable to environmental factors such as temperature, pH, sunlight, wind and other environmental factors. To understand and know the effect of wastewater conditions on the process of degradation of organic material, so we were performed research on the distribution model of the concentration of organic material 1-dimension (1-D), it was represented by the Biochemical Oxygen Demand (BOD). In this case, the BOD concentration of the flow one-direction on pond would be studied their changes through time. Changes in 1-D BOD concentration through time could be represented in the form of partial differential equations. Because of the research was conducted in the stabilization ponds, which it is domain simple field with a structured grid discretization process, so the numerical method used for the solving of the model is finite difference method FTCS. Then, the validation of the model was did using the BOD concentration data is derived from the Wastewater Treatment Plant (WWTP), Sewon, Bantul, D.I. Yogyakarta.
2. Materials and Methods
2.1. Advection-Diffusion Equation
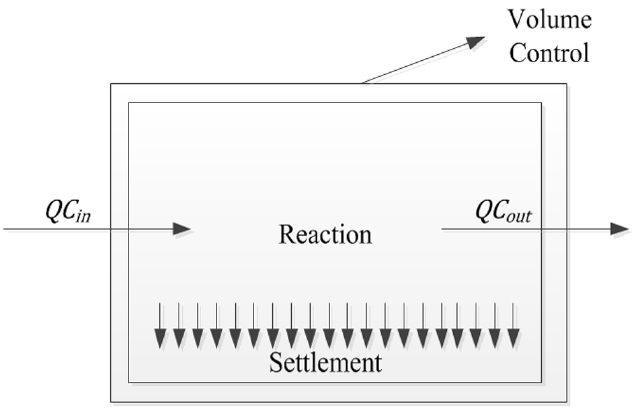
BOD concentration in a fluid flow through a region in the space which was known as the volume control [16]. The flow in the form of BOD system at the volume control with one-dimensional property of the flow and unsteady
, apply the integral conservation of mass as follows [17]:
ρiAiVi = M
with M is the mass flow rate or rate of mass.
The rate of mass (M) is the mass that flows per unit volume (kg/s). Volumetric flow rate (Q) is the volume flow per unit time (m3/s). The concentration (C) is the measure of a component in a mixture or solution or moles which was expressed as mass per unit volume (kg/m3). Density (ρ) is mass per unit volume (kg/m3). The relationship between the rate of mass and volumetric rate are:
So, Eq. (4) becomes:
Eq. (6) in accordance with the law of conservation of mass which states that mass can not be created nor destroyed. For a volume control, conservation of mass can be expressed as [16]:
The mechanism of transport of pollutants (BOD) in the ponds can be shown in Fig. 1.
Mass balance equations of BOD in a pond flow as shown in Fig. 1 states that the form of conservation of mass as follows:
Eq. (8) to the volume control with details known dimensions, it can be written mathematically as in Eq. (6) as follows:
with m = VC, so:
V in equation is a system volume that meets the space of control volume, then the value of V is constant. The Eq. (10) can be written as:
Solute mass flux in the x direction are transported through two mechanisms carrier (transport), namely advection and diffusion which can be written as follows:
Transport mass flux by advection: uC
Transport mass flux by diffusion:
The reaction mechanism is not considered, because BOD is assumed not react with any material in a flow of them. Similarly the settling mechanism, BOD in pond assumed no precipitation occurs or decay.
By multiplying both sides in Eq. (11) by a factor of 1/V, the equation becomes:
The term
and
respectively is the inflow and outflow with the advection and diffusion mechanisms. All of the term in the mass balance is directed into the form of the mass flux in the control volume as follows:
Therefore, the mass balance of a material dissolved by advection and diffusion mechanisms can be written as follows:
thus obtained:
Eq. (20) is an advection-diffusion equation without any reaction and settlement.
2.2. Finite Difference Method Forward Time Central Space
Finite difference method is one of method used to solve partial differential equations numerically. Finite difference method uses Taylor series to approximate the derivatives existing on partial differential equations into a form of linear equation [18]. The Taylor series approach is:
FTCS method is one of the finite difference method with the derivative on partial differential equations respect to time was using forward different schemes and its derivatives space using center different schemes [19].
Approximation derivative with respect to time with a forward different approach is as follows:
Then the derivatives space with center difference approach are as follows:
Then for the derivatif second order is:
2.3. Wastewater Treatment Plant (WWTP) Sewon
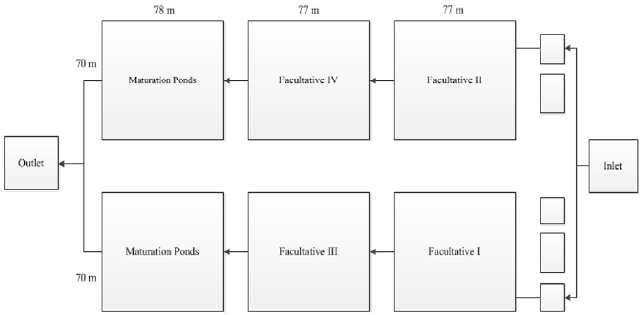
The research was conducted on the WWTP Sewon, Bantul, D.I. Yogyakarta. WWTP Sewon built to collect domestic waste amounted to 15,500 m3/d from the city of Yogyakarta and surrounding areas to be treated to re-usable. IPAL Sewon was built in 1993–1998, as a way to cope with contamination of wastewater in the region of Yogyakarta, five of the districts of Sleman, and three of the districts of Bantul. Wastewater that enters IPAL Sewon was processed through 6 aeration pond, namely facultative 1, facultative 2, facultative 3, facultative 4 and 2 maturation ponds. WWTP effluent poured into the river Bedog. For more details, waste stabilization ponds can be seen in Fig. 2.
The data collection of samples carried out in one of the facultative pond using discretization sketch as shown in Fig. 3.
The BOD concentration data which was obtained from sampling in WWTP Sewon is summarized in Table 1.
BOD concentration data as shown in Table 1 are not only used as an initial value and boundary value on completion of advection-diffusion equation. This data is also used to estimate the diffusivity coefficient parameters which done using merging two theories, namely Eyring and hydrodynamic theory of Stokes-Einstein equation [16], as follows:
Before performing parameter estimation, first determine the value of C,T,μ by using Least Square method. Least Square method is needed to obtain the relationship between variables empirically to minimize the effect of measurement error of the variable [20].
The value of parameter estimate which obtained are:
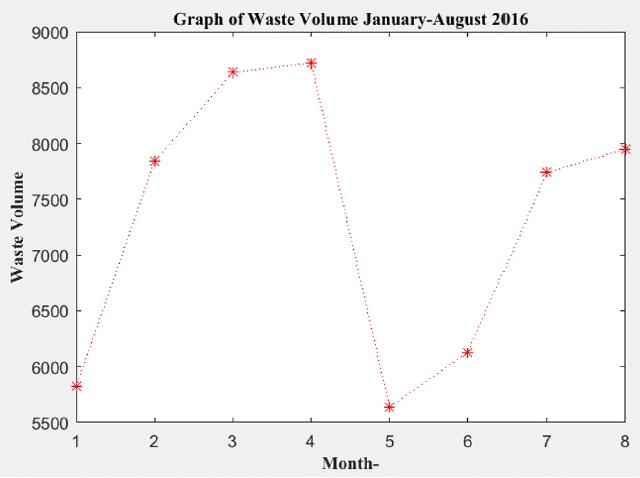
In addition to BOD concentration data, we also have obtained data on the volume of waste in January-August 2016 which is summarized in Table 2 and the graph in Fig. 4.
Based on Table 2 and Fig. 4, it can be concluded that the volume of waste water was different every time. It was influenced by various factors, such as temperature, weather, time and other factors.
Based on these data, it can be formulated flow velocity in the horizontal direction which estimated constant is as follows:
with,
u: Flow velocity in the horizontal direction (LT−1)
Db: Debit or Average Wastewater Volume (L3T−1)
l: Width Ponds (L)
h: Height Ponds (L)
The calculation is:
Because of the required flow velocity is the speed per hour, so:
So, the value of flow velocity is 1.0875 m/h.
3. Results and Discussion
In numerically, the completion of advection-diffusion equation is done by changing the equation into a discrete form as in Eq. (25), namely:
Then, Eq. (26) is simplified as follows:
Suppose:
then,
Furthermore, the completion is done by changing the discrete equation into the form of a matrix.
Suppose:
then it was obtained:
Eq. (31) with 1 < i < 5, then the system of equations is obtained as follows:
If presented in the form of a matrix, the equation system becomes:
with,
Boundary values in this study was assumed to be constant.
Therefore, it was obtained matrix form as follows:
Based on the above, it could be concluded that in order to calculate the value of the BOD concentration at a particular time, namely
, we required initial value and boundary value
which was known until the desired iteration. Because of the calculation process was very long, it was solved numerically using MATLAB.
Based on algorithms of completion of models, the initial value, boundary values and the other inputs, then simulation results could be summarized in Fig. 5.
This simulation result was the result of solving advection-diffusion equation by using finite difference method FTCS scheme. This method was applied to MATLAB software with syntax of finite difference method FTCS for advection-diffusion equation, input of initial value and boundary value. The output of this MATLAB syntax were the BOD concentration value on the grids with the different time, and the graph with set down of the grid according to field condition.
Based on observations of in Fig. 5 looks a mass deployment process (diffusion). The value of the mass concentration in the middle of the flow an initially high, then it was slowly spreads and declining, mainly on the left edge of the pond. This could happen in the middle of ponds estimated because the aerator was works on the principle of mixing perfect. However, a decrease in the BOD concentration was relatively small. It could be seen from the changes in concentration levels in a span of 2 h.
Fig. 5 was also indicated that a point/grid of flow has a rate of mass concentrations constant from time to time. This could be seen at the point/grid about 46 meters away from the left edge of the pond. In addition, there was an increased concentration of BOD, namely in the flow of the right edge pond. The improvement occurred after the first 2 h, then it was constant about 8 h and was increased back to 24 h (a day). Increased the concentration of mass estimated because in this study only considere the pond as a straight line and not as a field. On the right edge of the pond was estimated to occur mass transfer processes (advection), BOD concentration of the various sides of the pond move in the same direction (the right edge of the pond), so that the flow of the pond on the right edge of the pond was be increase. But the process of advection was also estimated to be very slow.
Based on the numerical results and field data which was obtained, then it did the model validation process. This validation process was done by comparing the data of numerical calculations with data obtained from sampling at the WWTP Sewon, Bantul. The validation process was necessary to know how big the validity of the modeling done (data consistency between the numerical results with field data). Data which was validated is the point of a observation at the time t = 12.
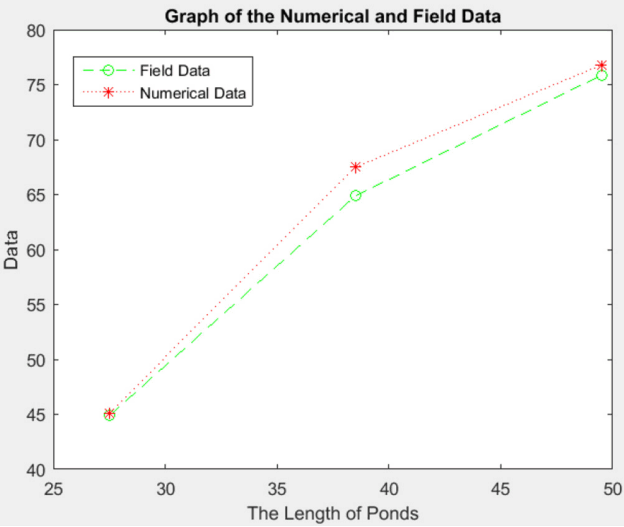
Comparison of numerical data and field data could be seen in Table 3.
According to table 3, there was differences between the data numerical results with field data. The average difference was 1.93%. To find out these differences more clearly, it could be seen in Fig. 6.
To know connection between research results with the results of the calculation, the correlation coefficient was determined by the formula:
The calculation of correlation coefficient of 0.998. It states that 99.8% of numerical data in accordance with the field data.
4. Conclusions
This article shows that an advection diffusion equation in a structured domains such as waste stabilization ponds could be solved using finite difference methods FTCS scheme. In this study, the advection-diffusion equation was the equation of a flow system of BOD on a control volume assumed in the absence of reaction and precipitation.
Finite different FTCS method was discretization method of advection-diffusion equation with advanced difference scheme on time derivative, and middle difference scheme on space derivative. Discrete sketches according to finite difference methods FTCS was used to obtain objective research data on one of the facultative ponds. This method was applied to MATLAB software with input of initial value and boundary value. The output of this MATLAB syntax were the BOD concentration value on the grids with the different time, and the graph with set down of the grid according to field condition.
The result of the simulation shows that the advection and diffusion process in the flow of 1-direction waste stabilization pond was occurs very slowly. This was evident from the relatively small decrease in BOD concentrations on the left edge of the pond. But on the right edge of the pond, there was an increase in BOD concentration. The increase of mass concentration was estimated because in this study only consider the pond as a straight line and not as a field of ponds. On the right edge of the pond was estimated to occur the process of mass transfer (advection). BOD concentration from various sides of the pond moved in the same direction (the right edge of the pond), so that the flow on the right edge of the pond to increase. But the occurrence of this advection process was also estimated very slowly. In addition, temperature, pH, aerator and other factors also have a considerable effect.
Numerical results and field data obtained were compared as a form of validation of models and it was found a difference of 1.93%. It was claimed that the numeric data was not much different with the field data. This was reinforced by the correlation coefficient of 0.998, meaning that 99.8% of numerical data in accordance with the field data.
Other similar studies should be minimize the grid on the domain in order to obtain maximum results. Use of other numerical methods are also very advised to obtain results more in line with the real situation.